Codeforces Gym 101505C : Cable Connection （计算几何）

题目链接

题意：给出第一象限的N个点，存在一直线x/a+y/b=1(a>0,y>0)使得所有点都在这条直线下面，求 min{sqrt(a^2+b^2)}

显然，这样的直线必然经过这N个点中的某一个（可用反证法证得），所以先对只有一个点的情况进行分析。

当只有一个点P(x0,y0)时，易得

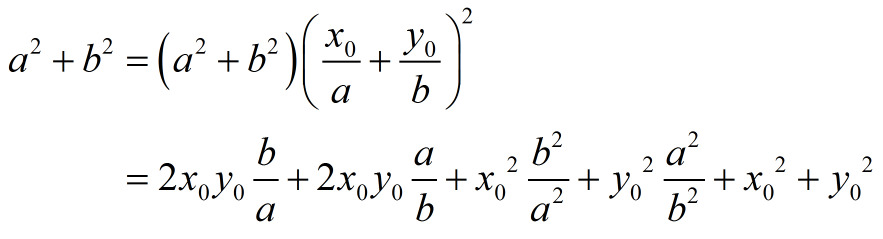
此时设t=a/b，可知，a^2+b^2可写成两个凹函数相加的形式，故可用三分法求解。

所以N个点的情况就可解了。容易想到，只需要考虑凸包上位于右上侧的点（满足该点的左上方右下方都有点），那么该点就有成为“关键的点”的可能，至于三分时的自变量的范围，就根据这个点的前后两个点来得到即可。

#include<bits/stdc++.h>
using namespace std;

const double eps=1e-;
const double inf=2e6;
int dcmp(double x)
{
    if(fabs(x)<eps) return ;
    else return x<? -:;
}

struct Point
{
    double x,y;
    Point(double x_=,double y_=)
    {
        x=x_,y=y_;
    }
    Point operator -(const Point& rhs)
    {
        return Point(x-rhs.x,y-rhs.y);
    }
    bool operator<(const Point& rhs)const
    {
        return x<rhs.x||x==rhs.x&&y<rhs.y;
    }
};
typedef Point Vector;
double Cross(Vector A,Vector B)
{
    return A.x*B.y-A.y*B.x;
}
double Area2(Point A,Point B,Point C)
{
    return Cross(B-A,C-A);
}
int ConvexHull(Point *p,int n,Point *ch)
{
    sort(p,p+n);
    int m=;
    for(int i=; i<n; i++)
    {
        while(m>&&dcmp(Area2(ch[m-],ch[m-],p[i]))<=) --m;
        ch[m++]=p[i];
    }
    int k=m;
    for(int i=n-; i>=; --i)
    {
        while(m>k&&dcmp(Area2(ch[m-],ch[m-],p[i]))<=) --m;
        ch[m++]=p[i];
    }
    return n>? m-:m;
}
//=============================================================
const int maxn=1e6+;
Point p[maxn],ch[maxn];
double k[maxn];

double xielv(Point A,Point B)
{
    if(dcmp(A.x-B.x)==) return -inf;
    else return (A.y-B.y)/(A.x-B.x);
}
double cal(Point P,double P_k)
{
    double a=P.x-P.y/P_k;
    double b=P.y-P.x*P_k;
    return sqrt(a*a+b*b);
}
double sanfen(Point P,double k1,double k2)
{
    double l=k1,r=k2;
    while(r-l>eps)
    {
        double mid=(l+r)/;
        double f1=cal(P,mid);
        double midmid=(mid+r)/;
        double f2=cal(P,midmid);
        if(f1<f2)    r=midmid;
        else    l=mid;
    }
    return cal(P,l);
}

int main()
{
    int n,m;
    while(~scanf("%d",&n))
    {
        double ans=inf;
        double maxx=,maxy=;
        for(int i=; i<n; i++)    //读点
        {
            scanf("%lf%lf",&p[i].x,&p[i].y);
            maxx=max(maxx,p[i].x),maxy=max(maxy,p[i].y);
        }
        p[n++]=Point(maxx,),p[n++]=Point(,maxy);    //加点，便于处理
        m=ConvexHull(p,n,ch);    //求凸包
        for(int i=; i<m; i++) k[i]=xielv(ch[i],ch[(i+)%m]); //求斜率
        for(int i=; i<m; i++)
            if(ch[i].x>=ch[(i+)%m].x&&ch[i].y<=ch[(i+)%m].y && ch[(i+)%m].x>=ch[(i+)%m].x&&ch[(i+)%m].y<=ch[(i+)%m].y)
                ans=min(ans,sanfen(ch[(i+)%m],k[i],k[(i+)%m]));
        printf("%.3lf\n",ans+eps);
    }
}