【CF1252K】Addition Robot（线段树，矩阵乘法）

题意：

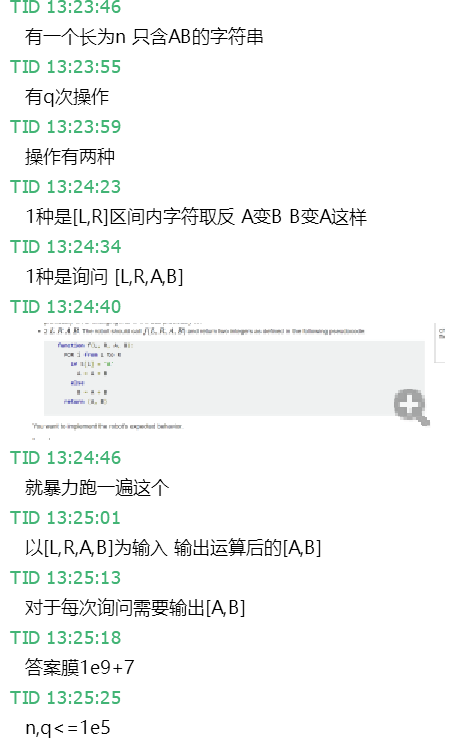
思路：因为线段树上每一段的矩阵之积只有两种，预处理一下，翻转的时候下传tag然后把另一种可能性换上来就好

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 typedef unsigned int uint;
 typedef unsigned long long ull;
 typedef long double ld;
 typedef pair<int,int> PII;
 typedef pair<ll,ll> Pll;
 typedef vector<int> VI;
 typedef vector<PII> VII;
 //typedef pair<ll,ll>P;
 #define N  200010
 //#define M  200010
 #define INF 1e9
 #define fi first
 #define se second
 #define MP make_pair
 #define pb push_back
 #define pi acos(-1)
 #define mem(a,b) memset(a,b,sizeof(a))
 #define rep(i,a,b) for(int i=(int)a;i<=(int)b;i++)
 #define per(i,a,b) for(int i=(int)a;i>=(int)b;i--)
 #define lowbit(x) x&(-x)
 #define Rand (rand()*(1<<16)+rand())
 #define id(x) ((x)<=B?(x):m-n/(x)+1)
 #define ls p<<1
 #define rs p<<1|1

 const ll MOD=1e9+,inv2=(MOD+)/;
       double eps=1e-;
       int dx[]={-,,,};
       int dy[]={,,-,};

 struct Ma
 {
     int n=,m=;
     ll a[][];
     void init()
     {
         n=m=;
         mem(a,);
     }
     Ma operator +(Ma b) const
     {
         Ma c;
         c.n=n; c.m=m;
         rep(i,,n-)
          rep(j,,m-) c.a[i][j]=a[i][j]+b.a[i][j];
         return c;
     }
     Ma operator *(Ma b) const
     {
         Ma c;
         c.init();
         c.n=n; c.m=b.m;
         rep(i,,n-)
         rep(j,,b.m-)
         rep(k,,m-) c.a[i][j]=(c.a[i][j]+a[i][k]*b.a[k][j]%MOD)%MOD;
         return c;
     }
 };

 Ma t[N<<][],M[],one,ans;
 int b[N],tag[N];
 char s[N];

 int read()
 {
    int v=,f=;
    char c=getchar();
    while(c<||<c) {if(c=='-') f=-; c=getchar();}
    while(<=c&&c<=) v=(v<<)+v+v+c-,   c=getchar();
    return v*f;
 }

 void pushdown(int p)
 {
     if(tag[p])
     {
         swap(t[ls][],t[ls][]);
         swap(t[rs][],t[rs][]);
         tag[ls]^=;
         tag[rs]^=;
         tag[p]=;
     }
 }

 void pushup(int p)
 {
     t[p][]=t[ls][]*t[rs][];
     t[p][]=t[ls][]*t[rs][];
 }

 void build(int l,int r,int p)
 {
     if(l==r)
     {
         t[p][]=M[b[l]];
         t[p][]=M[b[l]^];
         tag[p]=;
         return;
     }
     int mid=(l+r)>>;
     build(l,mid,ls);
     build(mid+,r,rs);
     pushup(p);

 }

 void update(int l,int r,int x,int y,int p)
 {
     if(x<=l&&r<=y)
     {
         tag[p]^=;
         swap(t[p][],t[p][]);
         return;
     }
     pushdown(p);
     int mid=(l+r)>>;
     if(x<=mid) update(l,mid,x,y,ls);
     if(y>mid) update(mid+,r,x,y,rs);
     pushup(p);
 }

 Ma query(int l,int r,int x,int y,int p)
 {
     if(x<=l&&r<=y) return t[p][];
     pushdown(p);
     int mid=(l+r)>>;
     Ma res=one;
     if(x<=mid) res=res*query(l,mid,x,y,ls);
     if(y>mid) res=res*query(mid+,r,x,y,rs);
     return res;
 }

 int main()
 {
     //freopen("1.in","r",stdin);
     int n=read(),q=read();
     scanf("%s",s+);
     rep(i,,n) b[i]=s[i]-'A';
     M[].n=M[].m=M[].n=M[].m=one.n=one.m=ans.n=ans.m=;
     M[].a[][]=M[].a[][]=M[].a[][]=;
     M[].a[][]=M[].a[][]=M[].a[][]=;
     one.a[][]=one.a[][]=;
     build(,n,);

     while(q--)
     {
         int op=read();
         if(op==)
         {
             int x=read(),y=read();
             update(,n,x,y,);
         }
          else
          {
              int x=read(),y=read(),A=read(),B=read();
              Ma t=query(,n,x,y,);
             // printf("t=\n");
              //rep(i,0,1)
              //{
               //  rep(j,0,1) printf("%I64d ",t.a[i][j]);
               //  printf("\n");
              //}
              ans.a[][]=A;
              ans.a[][]=B;
              ans.a[][]=ans.a[][]=;
              ans=ans*t;
              printf("%I64d %I64d\n",ans.a[][],ans.a[][]);
          }
     }
     return ;
 }