红黑树的删除操作---以JDK源码为例

删除操作需要处理的情况：

1.删除的是红色节点，则删除节点并不影响红黑树的树高，无需处理。

2.删除的是黑色节点，则删除后，删除节点所在子树的黑高BH将减少1，需要进行调整。

节点标记：

• 正在处理的节点x
• 父节点p
• 兄弟节点s（sibling）
• 左侄子LN（Left Nephew）
• 右侄子RN（Right Nephew）

无需调整的情况（向上回溯时）

• 当前x为根节点，无论root为什么颜色，都将root染黑，rootOver。
• 当前x为红色，将其染黑，redOver。（增加所在子树黑高度，从而满足红黑树条件）。

删除左孩子情况：

1. s为红； s染红，p染黑，左旋p。
2. s为黑，LN与RN为黑； s染红，x回溯至p。
3. s为黑，LN为红，RN为黑； LN染黑，s染红，右旋p。
4. s为黑，LN随意，RN为红； s变为p的颜色，p和RN染黑，左旋p。

删除右孩子的情况和删除左孩子的情况相对称。

所有的情况为：



以删除左孩子为例，如下图，x为删除节点的后继节点。则p的左子树黑高度比右子树少1。若经过调整后，左右子树黑高恢复相等，则完成修复，否则，会转换为另一种情况，并按次方法继续进行修正。

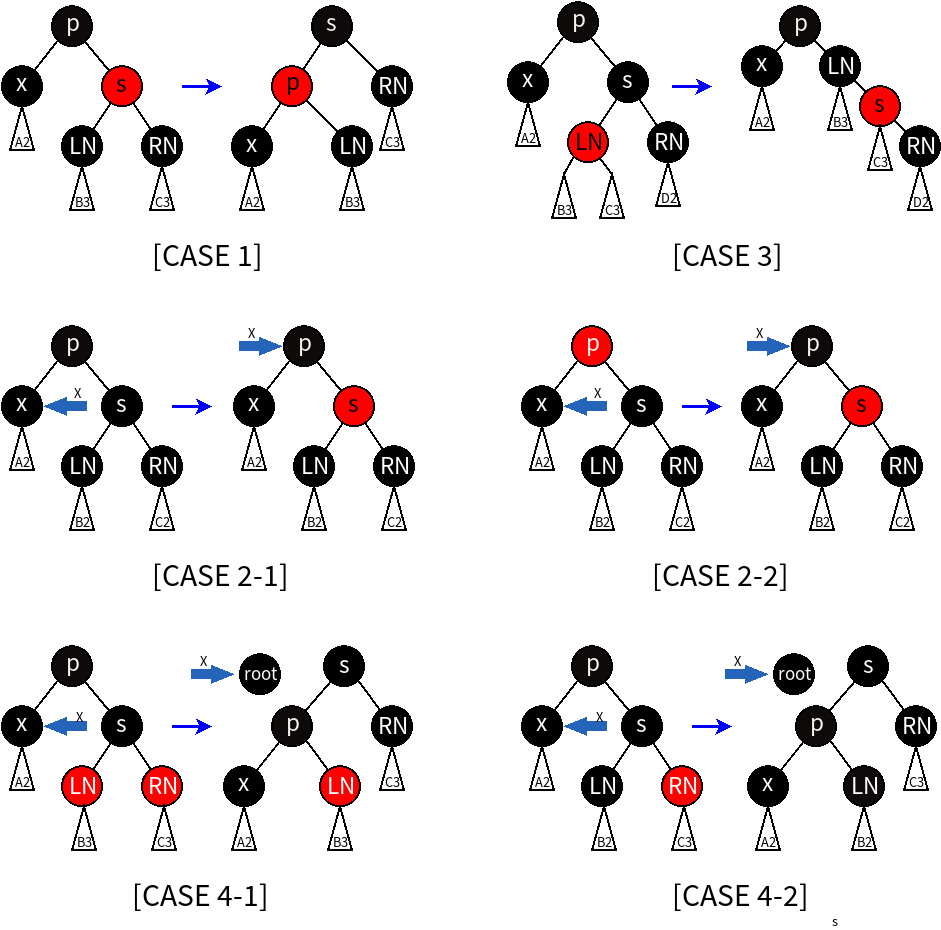
修正后情况的转换

情况转换的的原因：经调整后，左右子树的黑高度仍不相等，需要针对新的情况继续进行调整。

若修正后的左右子树黑高相同，则修正结束，无需情况转换。

转换如下：

Case 1 ==>> Case 2-2，Case 3,Case 4-1或 Case 4-2 不会引起黑高变化

Case 2-1 ==>> all Cases 当p为root节点时，会使整个树的黑高度减少1（唯一减少树黑高的情况）。

Case 2-2 ==>> redOver 并结束调整。

Case 3 ==>> Case 4-1或 Case 4-2;

Case 4 ==>> rootOver;

根据JDK源代码，分析函数对各种情况的处理方法。

    private void fixAfterDeletion(TreeMap.Entry<K, V> var1) {
        while(var1 != this.root && colorOf(var1)) {
            //若当前节点为红色或者到达根节点，则修正结束。
            TreeMap.Entry var2;
            if (var1 == leftOf(parentOf(var1))) {    //当前节点为左孩子
                var2 = rightOf(parentOf(var1));      //兄弟节点s
                if (!colorOf(var2)) {                //s为红 [Case 1]
                    setColor(var2, true);            //s染黑
                    setColor(parentOf(var1), false); //p染红
                    this.rotateLeft(parentOf(var1)); //左旋p
                    var2 = rightOf(parentOf(var1));  //更新兄弟s
                }

                if (colorOf(leftOf(var2)) && colorOf(rightOf(var2))) {
                    //LN 和 RN都为黑[Case 2]
                    //若从[Case 1]转换而来，则p为红[Case 2-2]
                    //但[Case 2]两种情况的处理策略相同
                    setColor(var2, false);            //s染红
                    var1 = parentOf(var1);            //x向上回溯
                } else { //LN 和 RN不全黑 [Case 3，4]
                    if (colorOf(rightOf(var2))) {    //RN黑[Case 3]
                        setColor(leftOf(var2), true);//LN染黑
                        setColor(var2, false);       //s染红
                        this.rotateRight(var2);      //右旋s
                        var2 = rightOf(parentOf(var1));//更新s为LN
                    }
                    //经[Case 3]修正后转换为[Case 4]
                    //[Case 4]分为两种情况，但修正方法相同
                    setColor(var2, colorOf(parentOf(var1)));//将s染成p的颜色
                    setColor(parentOf(var1), true);         //p染黑
                    setColor(rightOf(var2), true);          //RN染黑
                    this.rotateLeft(parentOf(var1));        //左旋p
                    var1 = this.root;                       //x回溯至根节点
                    //至此修正已基本完成（还有可能对根节点染黑）
                }
            } else {
                //当前节点为左孩子，对称情况
                var2 = leftOf(parentOf(var1));            //兄弟节点s
                if (!colorOf(var2)) {                     //兄弟节点为红[Case 1]
                    setColor(var2, true);                 //s染黑
                    setColor(parentOf(var1), false);      //p染红
                    this.rotateRight(parentOf(var1));     //p右旋
                    var2 = leftOf(parentOf(var1));        //更新s为LN
                }

                if (colorOf(rightOf(var2)) && colorOf(leftOf(var2))) {
                    //LN 和 RN都为黑[Case 2]
                    //若从[Case 1]转换而来，则p为红[Case 2-2]
                    //但[Case 2]两种情况的处理策略相同
                    setColor(var2, false);            //s染红
                    var1 = parentOf(var1);            //向上回溯
                } else { //LN 和 RN不全黑 [Case 3，4]
                    if (colorOf(leftOf(var2))) {      //LN黑，RN红[Case 3]
                        setColor(rightOf(var2), true);//RN染黑
                        setColor(var2, false);        //s染红
                        this.rotateLeft(var2);        //左旋s
                        var2 = leftOf(parentOf(var1));//更新s为LN
                    }
                    //经[Case 3]修正后转换为[Case 4]
                    //[Case 4]分为两种情况，但修正方法相同
                    setColor(var2, colorOf(parentOf(var1)));//s染成p的颜色
                    setColor(parentOf(var1), true);         //p染黑
                    setColor(leftOf(var2), true);           //LN染黑
                    this.rotateRight(parentOf(var1));       //右旋p
                    var1 = this.root;                       //x直接回溯到root
                    //至此修正已基本完成（还有可能对根节点染黑）
                }
            }
        }

        //根红色节点染黑，或者将根节点染黑
        setColor(var1, true);
    }

总结：

 红黑树节点删除后的“双黑”现象修正，虽然情况复杂，情况间转换也复杂，但这些转换都是为了修正节点删除产生的叶节点黑深度不相等。而黑深度相等是红黑树的规定之一，红黑树的规定可以确保树中节点的高效插入，搜索和删除操作。这些努力都是为了实现数据结构的良好性能。

后记

 学习红黑树的知识，始于阅读《STL源码剖析》中的第五章：关联式容器。关联式容器的底层数据结构是二叉搜索树，红黑树作为一种高效且通用的平衡二叉搜索树，被作为STL关联数据类的底层数据结构。在继续阅读关联是容器的源代码前，需要对红黑树有一个初步的认识。而且数据结构是高效算法的基石，也是STL的基础。

 在学习红黑树的过程中，我看了网上的视频，作者是以JDK源代码进行讲解的。在阅读相关JDK源代码时，发现JDK源代码也很清晰明了，而且JDK里提供了丰富的容器类。相比之下，STL中提供的容器类就略显单一和老旧。但是阅读STL源码依然是学习程序语言，类层次结构设计，设计模式，数据结构和算法等知识的良好方法。而瞻仰JDK代码是今后的努力方向。