最小生成树，Prim算法实现

最小生成树

所谓最小生成树，就是一个图的极小连通子图，它包含原图的所有顶点，并且所有边的权值之和尽可能的小。

首先看看第一个例子，有下面这样一个带权图：

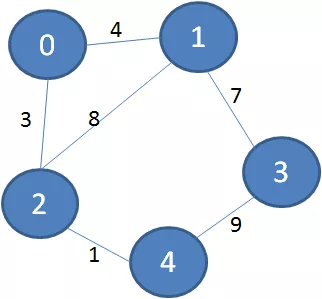
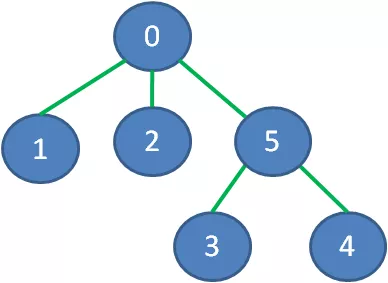
它的最小生成树是什么样子呢？下图绿色加粗的边可以把所有顶点连接起来，又保证了边的权值之和最小：

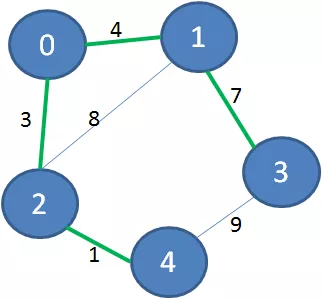
去掉那些多余的边，该图的最小生成树如下：

下面我们再来看一个更加复杂的带权图：

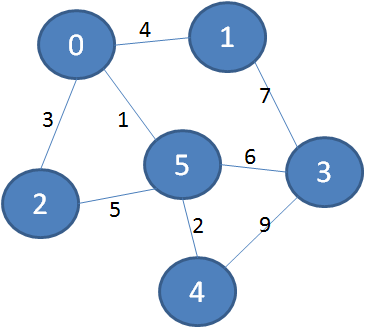
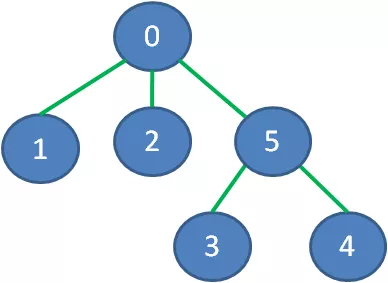
同样道理，下图绿色加粗的边可以把所有顶点连接起来，又保证了边的权值之和最小：

去掉那些多余的边，该图的最小生成树如下：

图的极小连通子图不需要回路，而是一个树形结构，所以人们才把它叫做最小生成【树】。图的最小生成树也不是唯一的，同一个图可以有多个不同的最小生成树，但是他们的权值之和是一样的。

最小生成树的用处可多了，比如我们要在若干个城市之间铺设道路，而我们的预算又是有限的，那么我们就需要找出成本最低的方式铺路，最小生成树的作用就来了。

怎样铺设才能保证成本最低呢？

城市之间的交通网就像一个连通图，我们并不需要在每两个城市之间都直接进行连接，只需要一个最小生成树，保证所有的城市都有铁路可以触达即可。

通常生成最小生成树常用的算法有两种，一种是 Kruskal 算法，另一种是 Prim 算法。下面介绍下 Prim 算法

Prim算法是如何工作的呢？

这个算法是以图的顶点为基础，从一个初始顶点开始，寻找触达其他顶点权值最小的边，并把该顶点加入到已触达顶点的集合中。当全部顶点都加入到集合时，算法的工作就完成了。Prim算法的本质，是基于贪心算法。

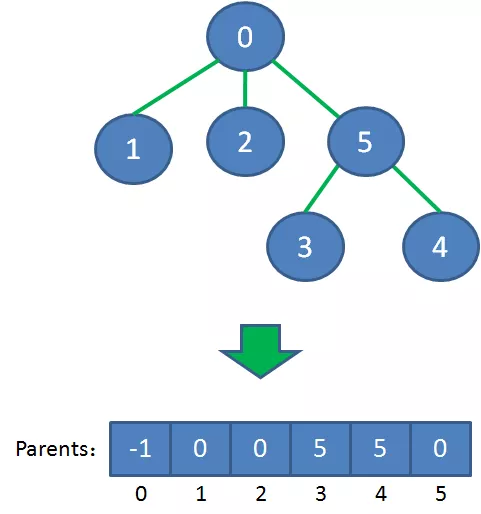
接下来说一说最小生成树的存储方式。我们最常见的树的存储方式，是链式存储，每一个节点包含若干孩子节点的指针，每一个孩子节点又包含更多孩子节点的指针：

这样的存储结构很清晰，但是也相对麻烦。为了便于操作，我们的最小生成树用一维数组来表达，数组下标所对应的元素，代表该顶点在最小生成树当中的父亲节点。（根节点没有父亲节点，所以元素值是-1）

下面让我们来看一看算法的详细过程：

1.选择初始顶点，加入到已触达顶点集合。

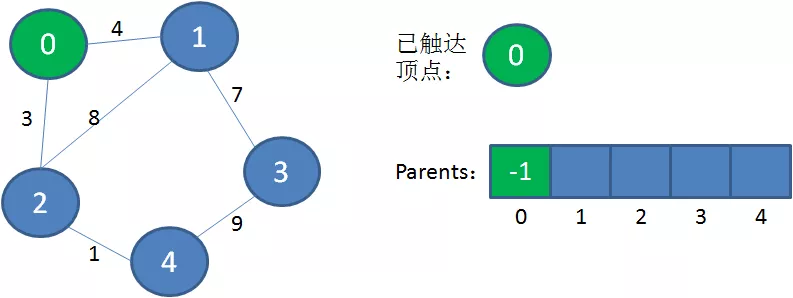
2.从已触达顶点出发，寻找到达新顶点的权值最小的边。显然从0到2的边权值最小，把顶点2加入到已触达顶点集合，Parents当中，下标2对应的父节点是0。

 

3.从已触达顶点出发，寻找到达新顶点的权值最小的边。显然从2到4的边权值最小，把顶点4加入到已触达顶点集合，Parents当中，下标4对应的父节点是2。

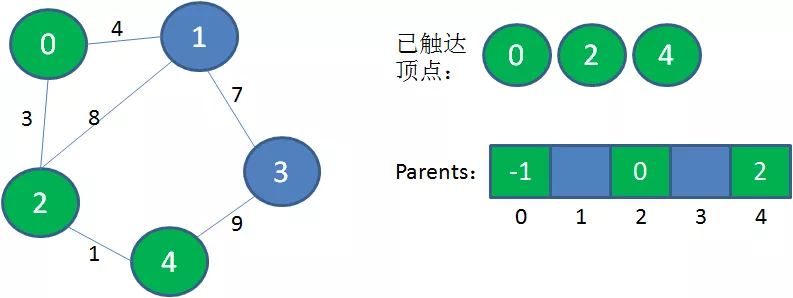
4.从已触达顶点出发，寻找到达新顶点的权值最小的边。显然从0到1的边权值最小，把顶点1加入到已触达顶点集合，Parents当中，下标1对应的父节点是0。

5.从已触达顶点出发，寻找到达新顶点的权值最小的边。显然从1到3的边权值最小，把顶点3加入到已触达顶点集合，Parents当中，下标3对应的父节点是1。

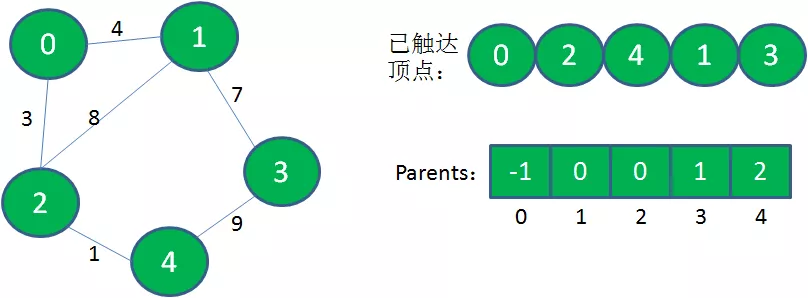
这样一来，所有顶点都加入到了已触达顶点集合，而最小生成树就存储在Parents数组当中。

Java：

import java.io.*;
import java.util.*;

class Test
{
    final static int INF = Integer.MAX_VALUE;
    public static int[] prim(int[][]matrix){
        List <Integer> reachedVertexList = new ArrayList<Integer>();
        //选择顶点0为初始顶点，放入已触达顶点集合中
        reachedVertexList.add(0);
        //创建最小生成树数组，首元素设为-1
        int[] parents = new int[matrix.length];
        parents[0]=-1;
        //边的权重
        int weight;
　　　　 //源顶点下标
        int fromIndex = 0;
　　　　 //目标顶点下标
        int toIndex =0;
        while(reachedVertexList.size() < matrix.length){
            weight =INF;
　　　　　　　//在已触达的顶点中，寻找到达新顶点的最短边
            for(Integer vertexIndex :reachedVertexList){
                for(int i =0;i <matrix.length;i++){
                    if(!reachedVertexList.contains(i)){
                        if(matrix[vertexIndex][i]<weight){
                            fromIndex =vertexIndex;
                            toIndex =i;
                            weight =matrix[vertexIndex][i];
                        }
                    }
                }
            }
            //确定了权值最小的目标顶点，放入已触达顶点集合
            reachedVertexList.add(toIndex);

　　　　　　　//放入最小生成树的数组
            parents[toIndex]=fromIndex;
        }
        return parents;
    }

    public static void main(String[]args){
        int[][]matrix =new int[][]{
            {0,4,3,INF,INF},
            {4,0,8,7,INF},
            {3,8,0,INF,1},
            {INF,7,INF,0,9},
            {INF,INF,1,9,0},
        };
        int[]parents =prim(matrix);
        System.out.println(Arrays.toString(parents));
    }

}

运行结果：

[-1, 0, 0, 1, 2]

这段代码当中，图的存储方式是邻接矩阵，在main函数中作为测试用例的图和对应的邻接矩阵如下：