BZOJ3566 : [SHOI2014]概率充电器

选个根把无根树转化成有根树，

设f[i]表示i不通电的概率

则

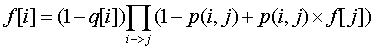
答案为对于枚举树根root进行DP后1-f[root]的和

直接算是O(n^2)的，但是n有500000，所以不能过。

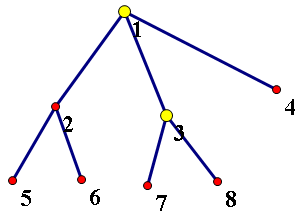
对于这样一棵以1为根的树，求出它的欧拉遍历序为

1->2->5->2->6->2->1->3->7->3->8->3->1->4->1

可以发现，按照这个序列，每次从上一个转移到下一个时只会在树上移动一步，

父子关系发生变化的也就只有这两个节点，

f[]值会发生变化的也就只有这两个节点。

设之前树根为r，现在准备转移到x上

在r中消去x对它的贡献

在x中加入r对它的贡献

由于是乘法，所以加入贡献只需要

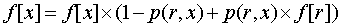
但是消去贡献就不能简单的除法了，因为可能有0

所以需要在每个点多维护

c0[i]表示i的孩子里有几个对它的贡献为0

f2[i]表示i的孩子里不是0的对它贡献的积

对于转移，有两种情况：

1.r是x的父亲：

-消去r对它父亲的贡献

-消去x对它父亲的贡献

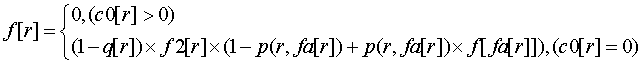
-加入r对它父亲的贡献

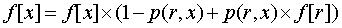
-加入x对它父亲的贡献

2.x是r的父亲：

-消去r对它父亲的贡献

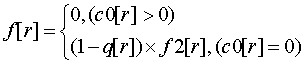
-加入r对它父亲的贡献

-消去x对它父亲的贡献

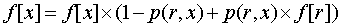
-加入x对它父亲的贡献

总时间复杂度$O(n)$

#include<cstdio>
#define N 500010
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
int n,i,x,y,z,g[N],ed,v[N<<1],nxt[N<<1],a[N<<1],eu,root,fa[N],c0[N];
double w[N<<1],q[N],f[N],ans,wf[N],f2[N],eps=1e-8;
bool vis[N];
inline bool is0(double x){return x<eps;}
inline void add(int x,int y,double z){v[++ed]=y;w[ed]=z;nxt[ed]=g[x];g[x]=ed;}
void dfs(int x,int pre){
  a[++eu]=x;f[x]=1-q[x];f2[x]=1;
  for(int i=g[x];i;i=nxt[i])if(v[i]!=pre){
    dfs(v[i],x),fa[v[i]]=x,wf[v[i]]=w[i],a[++eu]=x;
    double tmp=1-w[i]+w[i]*f[v[i]];
    f[x]*=tmp;
    if(is0(tmp))c0[x]++;else f2[x]*=tmp;
  }
}
inline void delson(int x){
  double tmp=1-wf[x]+wf[x]*f[x];
  if(is0(tmp))c0[fa[x]]--;else f2[fa[x]]/=tmp;
}
inline void addson(int x){
  double tmp=1-wf[x]+wf[x]*f[x];
  if(is0(tmp))c0[fa[x]]++;else f2[fa[x]]*=tmp;
}
inline void down(int r,int x){
  delson(r);
  delson(x);
  f[r]=c0[r]?0:(1-q[r])*f2[r]*(1-wf[r]+wf[r]*f[fa[r]]);
  addson(r);
  f[x]*=1-wf[x]+wf[x]*f[r];
  addson(x);
}
inline void up(int r,int x){
  delson(r);
  f[r]=c0[r]?0:(1-q[r])*f2[r];
  addson(r);
  delson(x);
  f[x]*=1-wf[r]+wf[r]*f[r];
  addson(x);
}
int main(){
  read(n);
  f[0]=1;
  for(i=1;i<n;i++)read(x),read(y),read(z),add(x,y,z/100.0),add(y,x,z/100.0);
  for(i=1;i<=n;i++)read(z),q[i]=z/100.0;
  dfs(1,0);
  ans=1-f[root=1];vis[1]=1;
  for(i=2;i<=eu;i++){
    if(fa[root]==a[i])up(root,a[i]);else down(root,a[i]);
    if(!vis[root=a[i]])vis[root]=1,ans+=1-f[root];
  }
  printf("%.6f",ans);
  return 0;
}