【经典算法】——KMP，深入讲解next数组的求解

我们在一个母字符串中查找一个子字符串有很多方法。KMP是一种最常见的改进算法，它可以在匹配过程中失配的情况下，有效地多往后面跳几个字符，加快匹配速度。

当然我们可以看到这个算法针对的是子串有对称属性，如果有对称属性，那么就需要向前查找是否有可以再次匹配的内容。

在KMP算法中有个数组，叫做前缀数组，也有的叫next数组，每一个子串有一个固定的next数组，它记录着字符串匹配过程中失配情况下可以向前多跳几个字符，当然它描述的也是子串的对称程度，程度越高，值越大，当然之前可能出现再匹配的机会就更大。

这个next数组的求法是KMP算法的关键，但不是很好理解，我在这里用通俗的话解释一下，看到别的地方到处是数学公式推导，看得都蛋疼，这个篇文章仅贡献给不喜欢看数学公式又想理解KMP算法的同学。

1、用一个例子来解释，下面是一个子串的next数组的值，可以看到这个子串的对称程度很高，所以next值都比较大。

位置i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
前缀next[i]	0	0	0	0	1	2	3	1	2	3	4	5	6	7	4	0
子串	a	g	c	t	a	g	c	a	g	c	t	a	g	c	t	g

申明一下：下面说的对称不是中心对称，而是中心字符块对称，比如不是abccba，而是abcabc这种对称。

（1）逐个查找对称串。

这个很简单，我们只要循环遍历这个子串，分别看前1个字符，前2个字符，3个... i个 最后到15个。

第1个a无对称，所以对称程度0

前两个ag无对称，所以也是0

依次类推前面0-4都一样是0

前5个agcta，可以看到这个串有一个a相等，所以对称程度为1前6个agctag，看得到ag和ag对成，对称程度为2

这里要注意了，想是这样想，编程怎么实现呢？

只要按照下面的规则：

a、当前面字符的前一个字符的对称程度为0的时候，只要将当前字符与子串第一个字符进行比较。这个很好理解啊，前面都是0，说明都不对称了，如果多加了一个字符，要对称的话最多是当前的和第一个对称。比如agcta这个里面t的是0，那么后面的a的对称程度只需要看它是不是等于第一个字符a了。

b、按照这个推理，我们就可以总结一个规律，不仅前面是0呀，如果前面一个字符的next值是1，那么我们就把当前字符与子串第二个字符进行比较，因为前面的是1，说明前面的字符已经和第一个相等了，如果这个又与第二个相等了，说明对称程度就是2了。有两个字符对称了。比如上面agctag，倒数第二个a的next是1，说明它和第一个a对称了，接着我们就把最后一个g与第二个g比较，又相等，自然对称成都就累加了，就是2了。

c、按照上面的推理，如果一直相等，就一直累加，可以一直推啊，推到这里应该一点难度都没有吧，如果你觉得有难度说明我写的太失败了。

当然不可能会那么顺利让我们一直对称下去，如果遇到下一个不相等了，那么说明不能继承前面的对称性了，这种情况只能说明没有那么多对称了，但是不能说明一点对称性都没有，所以遇到这种情况就要重新来考虑，这个也是难点所在。

（2）回头来找对称性

这里已经不能继承前面了，但是还是找对称成都嘛，最愚蠢的做法大不了写一个子函数，查找这个字符串的最大对称程度，怎么写方法很多吧，比如查找出所有的当前字符串，然后向前走，看是否一直相等，最后走到子串开头，当然这个是最蠢的，我们一般看到的KMP都是优化过的，因为这个串是有规律的。

在这里依然用上面表中一段来举个例子：

位置i=0到14如下,我加的括号只是用来说明问题：

(a g c t a g c )( a g c t a g c) t

我们可以看到这段，最后这个t之前的对称程度分别是：1，2，3，4，5，6，7,倒数第二个c往前看有7个字符对称，所以对称为7。但是到最后这个t就没有继承前面的对称程度next值，所以这个t的对称性就要重新来求。

这里首要要申明几个事实

1、t 如果要存在对称性，那么对称程度肯定比前面这个c 的对称程度小，所以要找个更小的对称，这个不用解释了吧，如果大那么t就继承前面的对称性了。

2、要找更小的对称，必然在对称内部还存在子对称，而且这个t必须紧接着在子对称之后。

如下图说明。

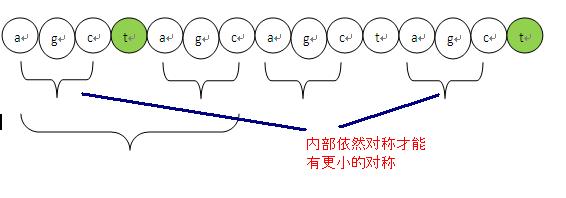
下面介绍《部分匹配表》是如何产生的。

首先，要了解两个概念："前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例，

　　－　"A"的前缀和后缀都为空集，共有元素的长度为0；

　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

从上面的理论我们就能得到下面的前缀next数组的求解算法。

void SetPrefix(const char *Pattern, int prefix[])

{

int len=CharLen(Pattern);//模式字符串长度。

prefix[0]=0;

for(int i=1; i<len; i++)

{

int k=prefix[i-1];

//不断递归判断是否存在子对称，k=0说明不再有子对称，Pattern[i] != Pattern[k]说明虽然对称，但是对称后面的值和当前的字符值不相等，所以继续递推

while( Pattern[i] != Pattern[k]  &&  k!=0 )

k=prefix[k-1];     //继续递归

if( Pattern[i] == Pattern[k])//找到了这个子对称，或者是直接继承了前面的对称性，这两种都在前面的基础上++

prefix[i]=k+1;

else

prefix[i]=0;       //如果遍历了所有子对称都无效，说明这个新字符不具有对称性，清0

}

}

通过这个说明，估计能够理解KMP的next求法原理了，剩下的就很简单了。我自己也有点晕了，实在不喜欢那些数学公式，所以用形象逻辑思维方法总结了一下。