最大似然估计 (MLE)与 最大后验概率(MAP)在机器学习中的应用
最大似然估计 MLE
给定一堆数据,假如我们知道它是从某一种分布中随机取出来的,可是我们并不知道这个分布具体的参,即“模型已定,参数未知”。
例如,对于线性回归,我们假定样本是服从正态分布,但是不知道均值和方差;或者对于逻辑回归,我们假定样本是服从二项分布,但是不知道均值,逻辑回归公式得到的是因变量y的概率P = g(x), x为自变量,通过逻辑函数得到一个概率值,y对应离散值为0或者1,Y服从二项分布,误差项服从二项分布,而非高斯分布,所以不能用最小二乘进行模型参数估计,可以用极大似然估计来进行参数估计; 因此最大似然估计(MLE,Maximum Likelihood Estimation)就可以用来估计模型的参数。MLE的目标是找出一组参数,使得模型产生出观测数据的概率最大:
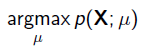
其中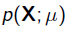 就是似然函数,表示在参数
就是似然函数,表示在参数 下出现观测数据的概率。我们假设每个观测数据是独立的,那么有
下出现观测数据的概率。我们假设每个观测数据是独立的,那么有
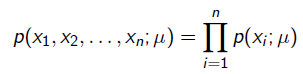
为了求导方便,一般对目标取log。 所以最优化对似然函数等同于最优化对数似然函数:
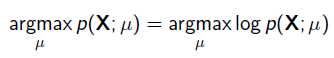
举一个抛硬币的简单例子。 现在有一个正反面不是很匀称的硬币,如果正面朝上记为H,方面朝上记为T,抛10次的结果如下:
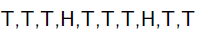
求这个硬币正面朝上的概率有多大?
很显然这个概率是0.2。现在我们用MLE的思想去求解它。我们知道每次抛硬币都是一次二项分布,设正面朝上的概率是 ,那么似然函数为:
,那么似然函数为:
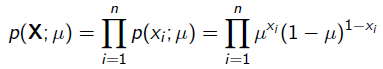
x=1表示正面朝上,x=0表示方面朝上。那么有:
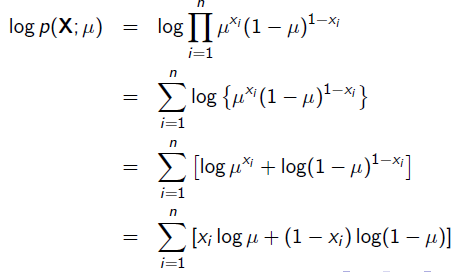
求导:
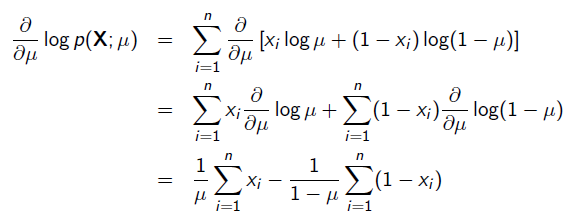
令导数为0,很容易得到:
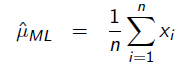
也就是0.2 。
最大后验概率 MAP
以上MLE求的是找出一组能够使似然函数最大的参数,即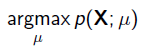 。 现在问题稍微复杂一点点,假如这个参数
。 现在问题稍微复杂一点点,假如这个参数 有一个先验概率呢?比如说,在上面抛硬币的例子,假如我们的经验告诉我们,硬币一般都是匀称的,也就是
有一个先验概率呢?比如说,在上面抛硬币的例子,假如我们的经验告诉我们,硬币一般都是匀称的,也就是 =0.5的可能性最大,
=0.5的可能性最大, =0.2的可能性比较小,那么参数该怎么估计呢?这就是MAP要考虑的问题。 MAP优化的是一个后验概率,即给定了观测值后使
=0.2的可能性比较小,那么参数该怎么估计呢?这就是MAP要考虑的问题。 MAP优化的是一个后验概率,即给定了观测值后使 概率最大:
概率最大:
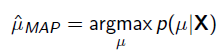
把上式根据贝叶斯公式展开:
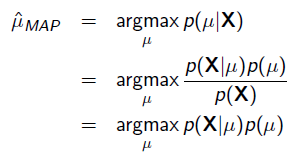
我们可以看出第一项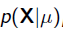 就是似然函数,第二项
就是似然函数,第二项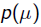 就是参数的先验知识。取log之后就是:
就是参数的先验知识。取log之后就是:
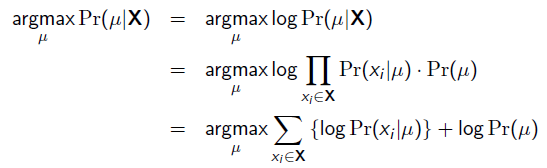
回到刚才的抛硬币例子,假设参数 有一个先验估计,它服从Beta分布,即:
有一个先验估计,它服从Beta分布,即:
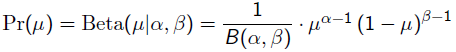
而每次抛硬币任然服从二项分布:
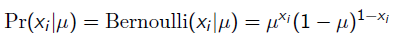
那么,目标函数的导数为:
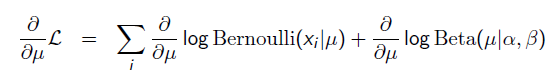
求导的第一项已经在上面MLE中给出了,第二项为:
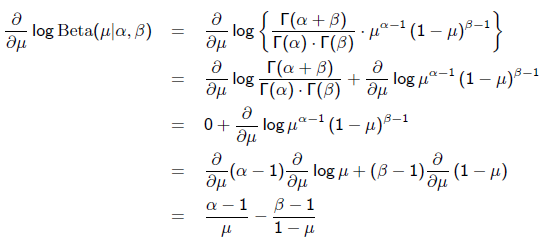
令导数为0,求解为:
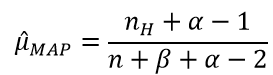
其中,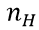 表示正面朝上的次数。这里看以看出,MLE与MAP的不同之处在于,MAP的结果多了一些先验分布的参数。
表示正面朝上的次数。这里看以看出,MLE与MAP的不同之处在于,MAP的结果多了一些先验分布的参数。
补充知识: Beta分布
Beat分布是一种常见的先验分布,它形状由两个参数控制,定义域为[0,1]
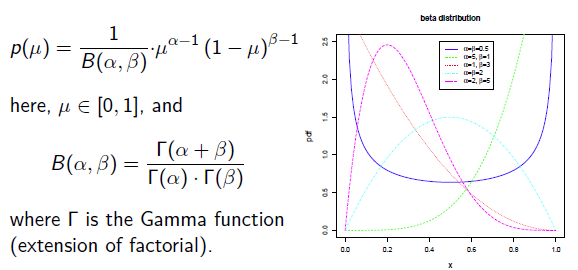
Beta分布的最大值是x等于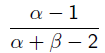 的时候:
的时候:
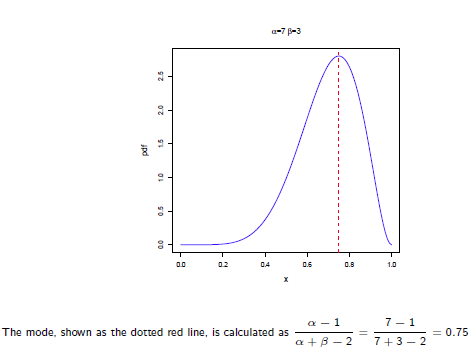
所以在抛硬币中,如果先验知识是说硬币是匀称的,那么就让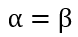 。 但是很显然即使它们相等,它两的值也对最终结果很有影响。它两的值越大,表示偏离匀称的可能性越小:
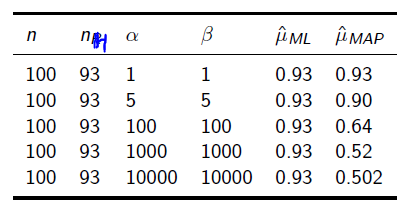
。 但是很显然即使它们相等,它两的值也对最终结果很有影响。它两的值越大,表示偏离匀称的可能性越小:
最大似然估计 (MLE)与 最大后验概率(MAP)在机器学习中的应用的更多相关文章
- 机器学习基础系列--先验概率 后验概率 似然函数 最大似然估计(MLE) 最大后验概率(MAE) 以及贝叶斯公式的理解
目录 机器学习基础 1. 概率和统计 2. 先验概率(由历史求因) 3. 后验概率(知果求因) 4. 似然函数(由因求果) 5. 有趣的野史--贝叶斯和似然之争-最大似然概率(MLE)-最大后验概率( ...
- 萌新笔记——Cardinality Estimation算法学习(二)(Linear Counting算法、最大似然估计(MLE))
在上篇,我了解了基数的基本概念,现在进入Linear Counting算法的学习. 理解颇浅,还请大神指点! http://blog.codinglabs.org/articles/algorithm ...
- 最大似然估计(MLE)与最小二乘估计(LSE)的区别
最大似然估计与最小二乘估计的区别 标签(空格分隔): 概率论与数理统计 最小二乘估计 对于最小二乘估计来说,最合理的参数估计量应该使得模型能最好地拟合样本数据,也就是估计值与观测值之差的平方和最小. ...
- Cardinality Estimation算法学习(二)(Linear Counting算法、最大似然估计(MLE))
在上篇,我了解了基数的基本概念,现在进入Linear Counting算法的学习. 理解颇浅,还请大神指点! http://blog.codinglabs.org/articles/algorithm ...
- 补充资料——自己实现极大似然估计(最大似然估计)MLE
这篇文章给了我一个启发,我们可以自己用已知分布的密度函数进行组合,然后构建一个新的密度函数啦,然后用极大似然估计MLE进行估计. 代码和结果演示 代码: #取出MASS包这中的数据 data(geys ...
- 最大似然估计 (MLE) 最大后验概率(MAP)
1) 最大似然估计 MLE 给定一堆数据,假如我们知道它是从某一种分布中随机取出来的,可是我们并不知道这个分布具体的参,即"模型已定,参数未知". 例如,我们知道这个分布是正态分布 ...
- 最大似然估计(MLE)与最大后验概率(MAP)
何为:最大似然估计(MLE): 最大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”.可以通过采样,获取部分数据,然后通过最大似然估计来获取已知模型的参数. 最大似然估计 ...
- 【模式识别与机器学习】——最大似然估计 (MLE) 最大后验概率(MAP)和最小二乘法
1) 极/最大似然估计 MLE 给定一堆数据,假如我们知道它是从某一种分布中随机取出来的,可是我们并不知道这个分布具体的参,即“模型已定,参数未知”.例如,我们知道这个分布是正态分布,但是不知道均值和 ...
- 深度学习中交叉熵和KL散度和最大似然估计之间的关系
机器学习的面试题中经常会被问到交叉熵(cross entropy)和最大似然估计(MLE)或者KL散度有什么关系,查了一些资料发现优化这3个东西其实是等价的. 熵和交叉熵 提到交叉熵就需要了解下信息论 ...
随机推荐
- python学习笔记011——内置函数sorted()
1 描述 sorted() 函数对所有可迭代的对象进行排序操作. sorted() 与sort()函数之间的区别 1 排序对象 sorted:所有可迭代对象的排序 sort:list列表的排序 2 返 ...
- CView类的使用
首先我们来写一个样例: 1.建一个win32简单应用程序,不要觉得这样就不能写出MFC程序,由于是不是MFC程序取决于调没调MFC函数. 2. 删除入口函数.仅仅留下#include "st ...
- js调用父级frame中的方法
父级frame中的方法: function hideOutline() { $("#outline").hide(); $("#content").attr(& ...
- sql server中bit字段实现取反操作
update Fct_StockMove set Disabled=Disabled^1 WHERE MoveId='DCE268E0-2CB3-4D17-AC4E-0046FB459CAD'; 1. ...
- app hybrid
package com.note.testcases; /** * * The MIT License (MIT) * * Copyright (c) 2016 Alejandro Gómez Mor ...
- DOA——ESPRIT算法
相位phei = 2*pi*f*d*sind(theta),因此理论上来讲测向的算法都可以用来测频. ESPRIT:Estimating signal parameters viarotational ...
- redis 只允许指定的额内网IP访问,其余的外网IP不允许访问
为了redis的安全,现在设定如下规则.只允许指定的服务器通过内网的方式访问.其余一律不准访问 因为redis登录额时候是不需要密码的,很不安全. 所以这里添加如下iptables规则 iptable ...
- Maven pom.xml 报 Missing artifact jdk.tools:jdk.tools:jar:1.7
linux中用eclipse 新建maven project,pom.xml中报Missing artifact jdk.tools:jdk.tools:jar:1.7 解决方法: 在pom.xml中 ...
- 国外程序员整理的Java资源大全
构建 这里搜集了用来构建应用程序的工具. Apache Maven:Maven使用声明进行构建并进行依赖管理,偏向于使用约定而不是配置进行构建.Maven优于Apache Ant.后者采用了一种过程化 ...
- JS动态增加删除UL节点LI
JS如何动态增加删除UL节点LI及相关内容. <ul id="ul"> <li id=1>11111111111111111<a href=" ...
