【原】Coursera—Andrew Ng机器学习—课程笔记 Lecture 7 Regularization 正则化

Lecture7　Regularization 正则化

7.1 过拟合问题 The Problem of Overfitting
7.2 代价函数 Cost Function
7.3 正则化线性回归 Regularized Linear Regression
7.4 正则化的逻辑回归模型 Regularized Logistic Regression

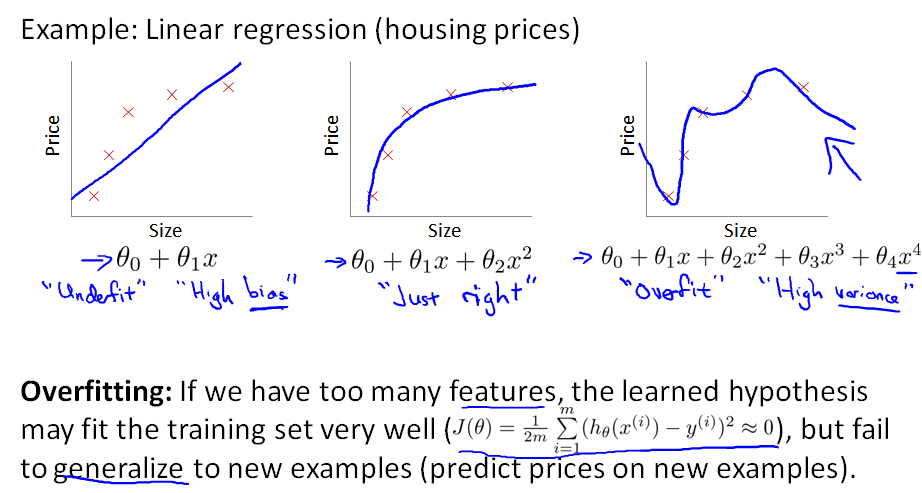
7.1 过拟合问题 The Problem of Overfitting

　　参考视频: 7 - 1 - The Problem of Overfitting (10 min).mkv

欠拟合/高偏差 underfitting 预测不准确
刚好　　 just right
过拟合/高方差 overfitting 泛化能力差

　回归问题：

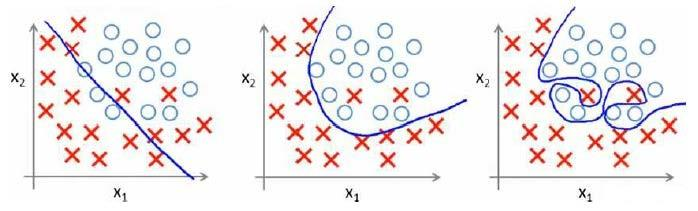
　　分类问题：

　　解决方法：

1) 减少 feature 的个数:

Manually select which features to keep.
Use a model selection algorithm .

2) 正则化

Keep all the features, but reduce the magnitude of parameters θj

Regularization works well when we have a lot of slightly useful features.

7.2 代价函数 Cost Function

　　参考视频: 7 - 2 - Cost Function (10 min).mkv

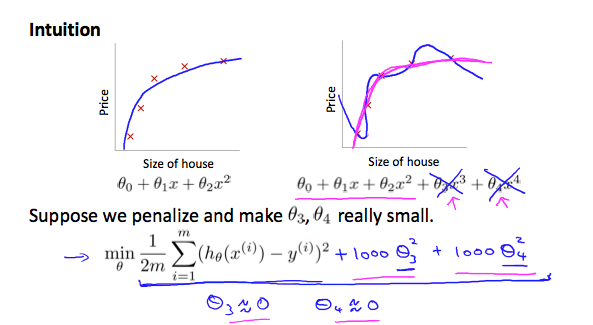
　　如果线性回归出现过拟合，曲线方程如下：

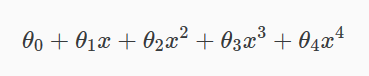
　　如果想消除高次幂项的影响，可以修改代价函数，在某些参数上设置一些惩罚，一定程度上减小这些参数的影响：

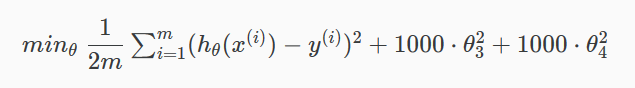
　　要使代价函数趋于0，则需降低θ₃和θ₄的值，因为二次项≥0，所以令它们为0时代价函数最小，降低了他们在hypothesis function的影响，从而减少了过拟合。这就是正则化的思想。

　　实际使用中，因为不知道具体应该惩罚那些参数。所以给所有参数都加一个系数 λ：

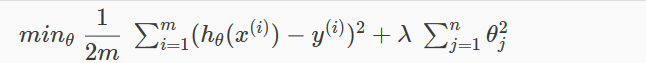
　　 λ or lambda 叫做 regularization parameter，加号后面这一项叫做 regularization term。
　　1）如果 λ = 0或者特别小，起不到作用，仍然过拟合。

　　1）如果 λ 选的太大，所有参数都遭到惩罚。最后假设方程可能变成 h(x) = θ_0，导致欠拟合 underfitting。

7.3 正则化线性回归 Regularized Linear Regression

　　参考视频: 7 - 3 - Regularized Linear Regression (11 min).mkv

　　正则化线性回归的代价函数为：

　　因为正则化不涉及到 θ₀，梯度下降算法如下：

　　对上面的算法第二个式子调整可得

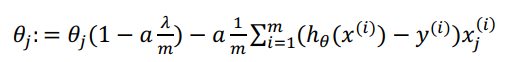( j ∈ 1,2 ... n)

　　正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令 θ减少了一个额外的值。

　　如果使用正规方程 Normal Equation方法，引入一个 (n+1)×(n+1)维的方阵L，正则化如下：

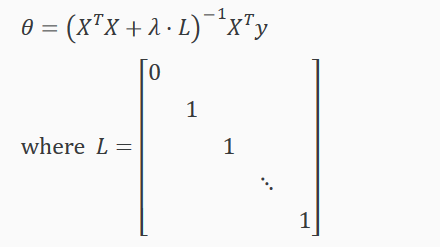
　　注：当 m < n 时，X^TX 不可逆non-invertible。但是当加上 λ⋅L，X^TX+ λ⋅L 变为可逆矩阵 invertible。

7.4 正则化的逻辑回归模型 Regularized Logistic Regression

　　参考视频: 7 - 4 - Regularized Logistic Regression (9 min).mkv

　　逻辑回归的代价函数为：

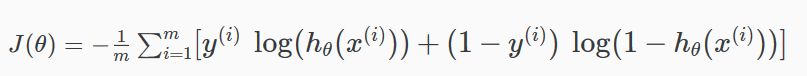
　　加上正则项之后：

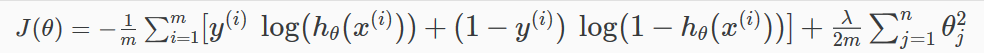
　　注：这个代价函数看上去同正则化线性回归的式子一样，但是两个 ℎ 不同，所以有很大差别。

θ₀不参与任何正则化
　　效果（蓝色线是正则化之前，粉色线是正则化之后）：

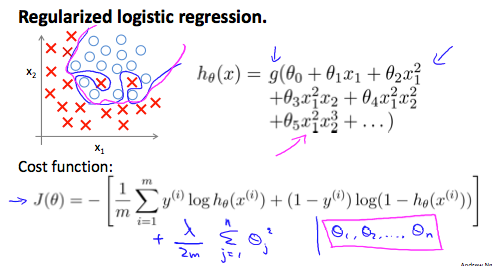
　　仍然可以用 fminuc 函数来求解代价函数最小化的参数，但我们实现的 costFunction 函数中进行了正则化：

　　python代码

 1 import numpy as np

 2 def costReg(theta, X, y, learningRate):

 3     theta = np.matrix(theta)

 4     X = np.matrix(X)

 5     y = np.matrix(y)

 6     first = np.multiply(-y, np.log(sigmoid(X*theta.T)))

 7     second = np.multiply((1 - y), np.log(1 - sigmoid(X*theta.T)))

 8     reg = (learningRate / (2 * len(X))* np.sum(np.power(theta[:,1:the

 9 ta.shape[1]],2))

10     return np.sum(first - second) / (len(X)) + reg