卡尔曼滤波总结——KF、EFK、UKF
1.用途
现实是我们的处理和测量模型都是非线性的,结果就是一个不规则分布,KF能够使用的前提就是所处理的状态是满足高斯分布的,为了解决这个问题,EKF是寻找一个线性函数来近似这个非线性函数,而UKF就是去找一个与真实分布近似的高斯分布。
- KF处理线性模型:
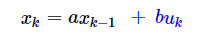
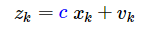
- EKF 通过雅克比和偏导数近似非线性模型,但是忽略了高阶导数:(强非线性系统下误差大,另一方面Jacobian矩阵的计算复杂)

- UKF 通过去点的方式近似非线性模型,因为没有用雅克比和偏导数,让计算变得更加简单,同时也没有忽略高阶导数项。
- PF不一定限于高斯分布
2.KF
卡尔曼滤波是一种高效率的递归滤波器(自回归滤波器), 它能够从一系列的不完全包含噪声的测量(英文:measurement)中,估计动态系统的状态,然而简单的卡尔曼滤波必须应用在符合高斯分布的系统中。
百度百科是这样说的,也就是说卡尔曼滤波第一是递归滤波,其次KF用于线性系统。
但经过研究和改进,出现了很多卡尔曼,如EKF(extended kalman filter)扩展卡尔曼,UKF(Unscented Kalman Filter)无迹卡尔曼等等。
而我们就来研究EKF,而EKF的中心思想就是将非线性系统线形化后再做KF处理。
状态方程
当我们从最简单的系统开始,我们假定k时刻的系统状态与k-1时刻有关,于是我们可以得到方程:
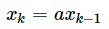
其中a为常量,但是当系统内部有噪声,我们称为过程噪声 ,计为w。所以方程可以写成:
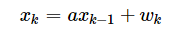
而我们实际观测的时候会出现观测噪声,于是我们将观测值计为Z,观测噪声为v,那我们可以把k时刻的观测值与系统状态值写成方程:
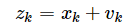
于是最简单的系统状态方程就有啦。
卡尔曼滤波算法核心思想在于预测+测量反馈,它由两部分组成,第一部分是 线性系统状态预测方程,第二部分是 线性系统观测方程。
这里系统的预测时候,我们要将通过系统状态方程计算的预测值作为先验信息,之后在观测部分在重新更新这个信息。
回头说状态的预测,我们引入一个符号 ^在相应的变量上表示该变量是预计值。再说一个新概念:新息。一个时间序列{X(t)}里,根据历史数据的预测值,新息是真实值减去预测值。
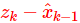
注:上有波浪线表示新息,也有用字母e表示的;上面尖的是预测值;无标注为真实值
我们给出一个优化过的预测值,新预测值 = 上一轮预测值(先验) + 权重 × 新息,即:
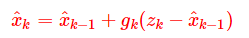
那下一个问题就是权重g是怎么计算得出的呢?答案是间接的从噪声里求得的。当我们将估计协方差叫做p,而传感器的协方差为r,我们通过这两个值计算权重。

既然获得了g,我们下一步将先验信息输入到上面的两个方程中获得后验预测值,也就是我们的输出值。
那整个计算步骤和过程就应该是这样的:

先预测后更新。具体计算过程和曲线生成可以参考levys教程的Part7。
之后我们再说更复杂一点的系统,系统地状态方程引入了输入量U。换句话说有一个U会时刻影响系统状态量。
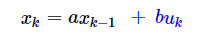
而观测到的观测值为
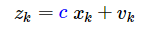
那我们新的计算方法就需要引入这两个新的变量,

同样是预测,更新,预测下一时刻,更新的计算方式。
而当系统用矩阵的方式写的状态方程,就需要以矩阵的方式计算。相同的数学公式及计算方法。如P的计算,
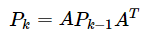
又如G,
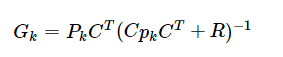
还有P的更新,
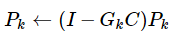

这样的话,我们的系统方程及计算步骤方式如下

需要注意的是我们使用的R是对测量误差v的协方差,当我们在引入一个Q代表过程噪声引起的误差时,可以使系统表现更好,即使Q很小,
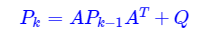
2.1 非线性系统之EKF
那如果系统是非线性的呢?我们如果将观测值Z计做X的非线性函数组成的,我们的模型可以改成。
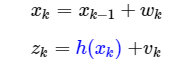
而我们的中心思想是将其线性化,如果我们使用函数一阶导为C来计算G和P。

最后系统复杂到这样的程度,

那我们就引入雅科比矩阵,雅各比矩阵就是方程矩阵对每一个变量的偏导数。
则在向量分析中,雅可比矩阵Jacobian matrix是该函数的所有分量( 个)对向量
的所有分量(
个)的一阶偏导数组成的矩阵。
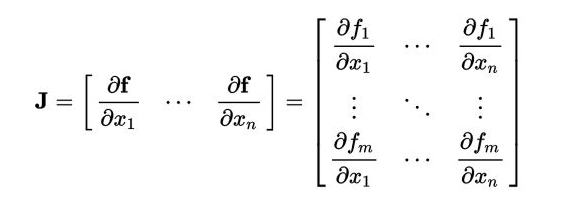
函数有 个分量,于是有
行。向量
有
个分量,于是有
列。
而最终,F为f方程的雅可比,H为h方程的雅可比。最终计算如下:
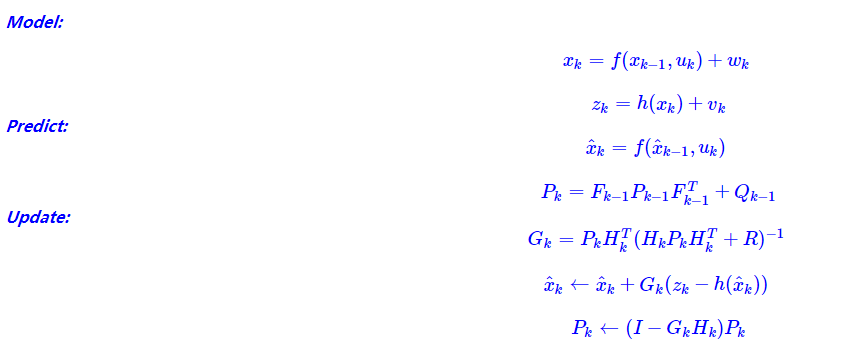
到这里简单的EKF就已经完成基本介绍啦。
3.UKF
3.1 模型
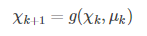
z(k+1)=h(x(k+1))
3.2 预测
1.预测sigma point(k+1步的分布点)
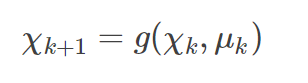
2.预测均值(Xpred)和方差(Ppred)
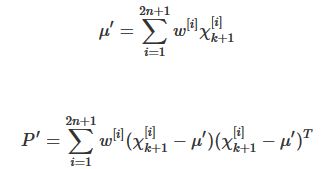
其中:
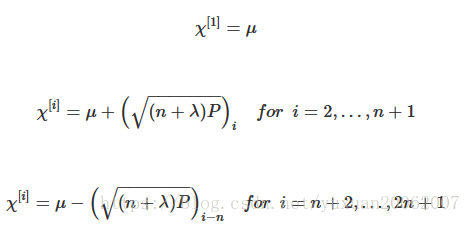
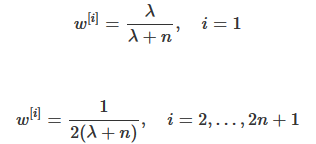
3.预测测量值
z(k+1)i=h(x(k+1)i)
从而zpred:
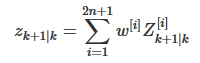
3.3更新
1.更新卡尔曼系数
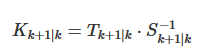
其中:
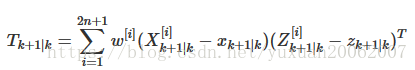

2.更新最终值:

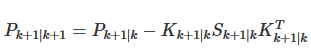
卡尔曼滤波总结——KF、EFK、UKF的更多相关文章
- 无人驾驶——4.控制之MPC模型预测控制
源自:<无人驾驶无人驾驶车辆模型预测控制>——龚建伟 参考:https://wenku.baidu.com/view/8e4633d519e8b8f67c1cb9fa.html 0.车辆模 ...
- 《视觉SLAM十四讲》第2讲
目录 一 视觉SLAM中的传感器 二 经典视觉SLAM框架 三 SLAM问题的数学表述 注:原创不易,转载请务必注明原作者和出处,感谢支持! 本讲主要内容: (1) 视觉SLAM中的传感器 (2) 经 ...
- 无损卡尔曼滤波UKF(3)-预测-生成Sigma点
无损卡尔曼滤波UKF(3)-预测-生成Sigma点 1 选择创建Sigma点 A 根据 已知上一个时间戳迭代出来的 后验状态 x_{k|k} 和后验协方差矩阵 P_{k|k} 他们代表当前状态的分布. ...
- 【算法基础】卡尔曼滤波KF
kalman filter KCF 尺度变化是跟踪中比较基本和常见的问题,前面介绍的三个算法都没有尺度更新,如果目标缩小,滤波器就会学习到大量背景信息,如果目标扩大,滤波器就跟着目标局部纹理走了,这两 ...
- slam kf
一.KF 1.从概率来理解概率估计因为希望整个运动估计较长时间内最优,所以反而会用最新的知识去更新之前的状态,就比如在做完当前帧的位姿估计的时候,修改局部地图的路标点.如果站在之前的状态上来考虑,用的 ...
- 扩展卡尔曼滤波(MRPT)
EKF relies on a linearisation of the evolution and observation functions which are good approximatio ...
- SLAM中的EKF,UKF,PF原理简介
这是我在知乎上问题写的答案,修改了一下排版,转到博客里. 原问题: 能否简单并且易懂地介绍一下多个基于滤波方法的SLAM算法原理? 目前SLAM后端都开始用优化的方法来做,题主想要了解一下之前基于 ...
- 卡尔曼滤波—Simple Kalman Filter for 2D tracking with OpenCV
之前有关卡尔曼滤波的例子都比较简单,只能用于简单的理解卡尔曼滤波的基本步骤.现在让我们来看看卡尔曼滤波在实际中到底能做些什么吧.这里有一个使用卡尔曼滤波在窗口内跟踪鼠标移动的例子,原作者主页:http ...
- 卡尔曼滤波跟踪 opencv
0 卡尔曼OPENCV 预测鼠标位置 卡尔曼滤波不要求信号和噪声都是平稳过程的假设条件.对于每个时刻的系统扰动和观测误差(即噪声),只要对它们的统计性质作某些适当的假定,通过对含有噪声的观测信号进行处 ...
随机推荐
- Python 多版本共存之pyenv
经常遇到这样的情况: 系统自带的 Python 是 2.6,自己需要 Python 2.7 中的某些特性: 系统自带的 Python 是 2.x,自己需要 Python 3.x: 此时需要在系统中安装 ...
- windows10 配置apache+php+mysql
apache配置就是个坑!!! 参考win10环境下配置win10Apache+PHP+MySQL环境的方法 注意:把所有"C:/apache2/..."都变为自己的apache目 ...
- 【Python系统学习】基础篇
这次真的是最后一次了!第三次滚Python的基础.走了太多弯路.认真一点!菜鸟! 教程 转义字符 \ 可以转义很多字符,比如\n表示换行,\t表示制表符,字符\本身也要转义,所以\\表示的字符就是\ ...
- terraform 阿里云基本使用
1. 预备环境 安装了terraform 的软件的操作系统(windows linux mac 均可) 具有阿里云账户的 access_key secret_key 2. 配置 // terrafor ...
- Linux下搭建 NFS
一.NFS简介 NFS是Network File System的缩写,即网络文件系统.一种使用于分散式文件协定,有SUN公司开发.功能是通过网络让不同的机器.不同的操作系统能够分享个人数据,让应用程序 ...
- CAN总线标准帧
CAN总线是一种串行数据通信协议,其通信接口中集成了CAN协议的物理层和数据链路层功能,可完成对通信数据的成帧处理,包括位填充.数据块编码.循环冗余检验.优先级判别等项工作. CAN总线结构 CAN总 ...
- thinkphp使用自定义类方法
1.通过Model调用 <?php /** * 积分模型 api接口 */ class ApiModel{ private $url = 'http://js.yunlutong.com/Cus ...
- bootstrap-datetimepicker如何只显示到日期
bootstrap-datetimepicker 一般都是设置到时分秒,有时候并不需要,怎么处理呢? minView: "month", //选择日期后,不会再跳转去选择时分秒 1 ...
- php对数组中的值进行排序
案例 <?php $a = array('1124','1125','1126'); $s1 = 1124; $s2 = 1125; $ks1 = array_search($s1,$a); $ ...
- VC++使用TCHAR
#ifdef _UNICODE #define tcout wcout #define tcin wcin #else #define tcout cout #define tcin cin #end ...
