ACM-线段树
http://blog.csdn.net/libin56842/article/details/8530197
基础可以看上面这篇文章
风格：
maxn是题目给的最大区间，而节点数要开4倍，确切的说……
lson和rson辨别表示结点的左孩子和右孩子。
PushUp(int rt)是把当前结点的信息更新到父节点
PushDown（int rt)是把当前结点的信息更新给孩子结点。
rt表示当前子树的根（root），也就是当前所在的结点。
思想：
对于每个非叶节点所标示的结点 [a,b]，其做孩子表示的区间是[a,(a+b)/2]，其右孩子表示[(a+b)/2,b].
构造：
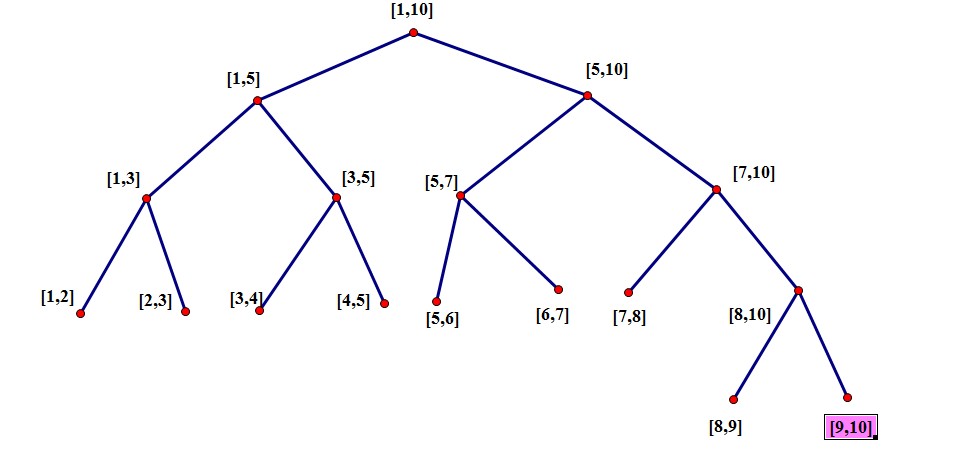
离散化和线段树：
题目：x轴上有若干个线段，求线段覆盖的总长度。
普通解法：设置坐标范围[min,max],初始化为0，然后每一段分别染色为1，最后统计1的个数，适用于线段数目少，区间范围小。
离散化的解法：离散化就是一一映射的关系，即将一个大坐标和小坐标进行一一映射，适用于线段数目少，区间范围大。
例如：[10000,22000],[30300,55000],[44000,60000],[55000,60000].
第一步：排序 10000 22000 30300 44000 55000 60000
第二部：编号 1 2 3 4 5 6
第三部：用编号来代替原数，即小数代大数 。
[10000,22000]~[1,2]
[30300,55000]~[3,5]
[44000,60000]~[4,6]
[55000,60000]~[5,6]
然后再用小数进行普通解法的步骤，最后代换回去。
线段树的解法：线段树通过建立线段，将原来染色O(n)的复杂度减小到 log（n），适用于线段数目多，区间范围小的情况。
离散化的线段树：适用于线段数目多，区间范围大的情况。
构造：
动态数据结构：
struct node{
node* left;
node* right;
……
}
静态全局数组模拟（完全二叉树）：
struct node{
int left;
int right;
……
}Tree[MAXN]
http://www.xuebuyuan.com/1470670.html
线段树主要用四种用法
单点更新：
模板：
单点增减，查询线段和
struct node
{
int l,r,c;
}T[MAXN*]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int l,int x)
{
if(T[x].l == T[x].r && T[x].l == l)
{
T[x].c += val;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
update(val,l,(x<<) + );
}
else
{
update(val,l,x<<);
}
PushUp(x);
} int n,m,ans; void query(int l,int r,int x)
{
if(T[x].l == l && T[x].r == r)
{
ans += T[x].c;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
query(l,r,(x<<)+);
}
else if(r<=mid)
{
query(l,r,(x<<));
}
else
{
query(l,mid,(x<<));
query(mid+,r,(x<<)+);
}
}
HDU 1166
#include <iostream>
#include <string>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <stack>
#include <queue>
#include <cctype>
#include <vector>
#include <iterator>
#include <set>
#include <map>
#include <sstream>
using namespace std; #define mem(a,b) memset(a,b,sizeof(a))
#define pf printf
#define sf scanf
#define spf sprintf
#define pb push_back
#define debug printf("!\n")
#define MAXN 55555
#define MAX(a,b) a>b?a:b
#define blank pf("\n")
#define LL long long
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define pqueue priority_queue
#define INF 0x3f3f3f3f struct node
{
int l,r,c;
}T[MAXN*]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int l,int x)
{
if(T[x].l == T[x].r && T[x].l == l)
{
T[x].c += val;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
update(val,l,(x<<) + );
}
else
{
update(val,l,x<<);
}
PushUp(x);
} int n,m,ans; void query(int l,int r,int x)
{
if(T[x].l == l && T[x].r == r)
{
ans += T[x].c;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
query(l,r,(x<<)+);
}
else if(r<=mid)
{
query(l,r,(x<<));
}
else
{
query(l,mid,(x<<));
query(mid+,r,(x<<)+);
}
} int main()
{
int t,i,kase=;
char d[];
sf("%d",&t);
while(t--)
{
mem(T,);
pf("Case %d:\n",kase++);
sf("%d",&n);
build(,n,);
for(i=;i<=n;i++)
{
int tmp;
sf("%d",&tmp);
update(tmp,i,);
} while (sf("%s",d) != EOF)
{
if (d[] == 'E') break;
int x, y;
sf("%d%d", &x, &y);
if (d[] == 'Q')
{
ans = ;
query(x,y,);
pf("%d\n",ans);
}
if (d[] == 'S') update(-y,x,);
if (d[] == 'A') update(y,x,);
}
}
return ;
}
单点替换，查询线段最高
模板：
struct node
{
int l,r,c;
}T[MAXN*]; void PushUp(int rt)
{
T[rt].c = max(T[rt<<].c,T[(rt<<)+].c);
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int l,int x)
{
if(T[x].l == T[x].r && T[x].l == l)
{
T[x].c = val;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
update(val,l,(x<<) + );
}
else
{
update(val,l,x<<);
}
PushUp(x);
} int n,m,ans; void query(int l,int r,int x)
{
if(T[x].l == l && T[x].r == r)
{
ans = max(ans,T[x].c);
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
query(l,r,(x<<)+);
}
else if(r<=mid)
{
query(l,r,(x<<));
}
else
{
query(l,mid,(x<<));
query(mid+,r,(x<<)+);
}
}
hdu 1754
这边要注意，输入字符不要用%c，会导致一些难以预料的问题
#include <iostream>
#include <string>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <stack>
#include <queue>
#include <cctype>
#include <vector>
#include <iterator>
#include <set>
#include <map>
#include <sstream>
using namespace std; #define mem(a,b) memset(a,b,sizeof(a))
#define pf printf
#define sf scanf
#define spf sprintf
#define pb push_back
#define debug printf("!\n")
#define MAXN 200005
#define MAX(a,b) a>b?a:b
#define blank pf("\n")
#define LL long long
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define pqueue priority_queue
#define INF 0x3f3f3f3f struct node
{
int l,r,c;
}T[MAXN*]; void PushUp(int rt)
{
T[rt].c = max(T[rt<<].c,T[(rt<<)+].c);
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int l,int x)
{
if(T[x].l == T[x].r && T[x].l == l)
{
T[x].c = val;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
update(val,l,(x<<) + );
}
else
{
update(val,l,x<<);
}
PushUp(x);
} int n,m,ans; void query(int l,int r,int x)
{
if(T[x].l == l && T[x].r == r)
{
ans = max(ans,T[x].c);
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
query(l,r,(x<<)+);
}
else if(r<=mid)
{
query(l,r,(x<<));
}
else
{
query(l,mid,(x<<));
query(mid+,r,(x<<)+);
}
} int main()
{
int t,i,kase=;
while(sf("%d%d",&n,&m)==)
{
build(,n,);
for(i=;i<=n;i++)
{
int tmp;
sf("%d",&tmp);
update(tmp,i,);
}
while (m--)
{
int x,y;
char d[]; sf("%s %d %d",d,&x, &y);
//pf("%s %d %d\n",d,x,y);
if (d[] == 'Q')
{
ans = ;
query(x,y,);
pf("%d\n",ans);
}
if (d[] == 'U') update(y,x,);
}
}
return ;
}
成段更新
(通常这对初学者来说是一道坎),需要用到延迟标记(或者说懒惰标记),简单来说就是每次更新的时候不要更新到底,用延迟标记使得更新延迟到下次需要更新or询问到的时候
http://blog.sina.com.cn/s/blog_a2dce6b30101l8bi.html
区间替换，求总和
数组要开4倍才够
第一种思路，标记
模板：
struct node
{
int l,r,c,f;
}T[MAXN<<2]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
//pf("%d %d\n",rt,T[rt].c);
} void PushDown(int rt,int m)
{
if(T[rt].f)
{
T[rt<<].f = T[(rt<<) + ].f = T[rt].f;
T[rt<<].c = T[rt].f * (m-(m>>));
T[(rt<<)+].c = T[rt].f * (m>>);
T[rt].f = ;
}
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
T[x].f = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
PushUp(x);
} void update(int val,int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
T[x].f = val;
T[x].c = val*(r-l+);
//pf("%d %d %d\n",T[x].c,l,r);
return;
}
PushDown(x,r-l+);
//pf("%d %d %d %d %d %d\n",val,L,R,l,r,x); int mid = (l + r)>>;
if (L <= mid)
{
update(val,L,R,l,mid,x<<);
}
if(R > mid)
{
update(val,L,R,mid+,r,x<<|);
}
PushUp(x);
}
第二种思路，杂色
struct node
{
int l,r,c;
}T[MAXN<<]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
} void PushDown(int rt)
{
if(T[rt].c != -)//如果该区间只有一种颜色
{
T[rt<<].c = T[rt<<|].c = T[rt].c;//由于后面必定对子树操作，所以更新子树的值等于父亲的值
T[rt].c = -;//由于该区域颜色与修改不同，而且不是给定区域，所以该区域必定为杂色
}
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int L,int R,int x)
{
if(T[x].c == val) return;//相同则不用修改了
if(T[x].l == L && T[x].r == R)//找到了区间，直接更新
{
T[x].c = val;
return;
}
PushDown(x); //父区间为杂色时对所有子节点进行操作
int mid = (T[x].l + T[x].r)>>;
if(L>mid)
update(val,L,R,x<<|);
else if(R<=mid)
update(val,L,R,x<<);
else
{
update(val,L,mid,x<<);
update(val,mid+,R,x<<|);
}
}
hdu 1698
http://www.tuicool.com/articles/j6N3eaz
这里链接的其实不对，要求总和，所以每个点不能初始化为1
#include <iostream>
#include <string>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <stack>
#include <queue>
#include <cctype>
#include <vector>
#include <iterator>
#include <set>
#include <map>
#include <sstream>
using namespace std; #define mem(a,b) memset(a,b,sizeof(a))
#define pf printf
#define sf scanf
#define spf sprintf
#define pb push_back
#define debug printf("!\n")
#define MAXN 100000 + 5
#define MAX(a,b) a>b?a:b
#define blank pf("\n")
#define LL long long
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define pqueue priority_queue
#define INF 0x3f3f3f3f struct node
{
int l,r,c,f;
}T[MAXN<<2]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
//pf("%d %d\n",rt,T[rt].c);
} void PushDown(int rt,int m)
{
if(T[rt].f)
{
T[rt<<].f = T[(rt<<) + ].f = T[rt].f;
T[rt<<].c = T[rt].f * (m-(m>>));
T[(rt<<)+].c = T[rt].f * (m>>);
T[rt].f = ;
}
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
T[x].f = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
PushUp(x);
} void update(int val,int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
T[x].f = val;
T[x].c = val*(r-l+);
//pf("%d %d %d\n",T[x].c,l,r);
return;
}
PushDown(x,r-l+);
//pf("%d %d %d %d %d %d\n",val,L,R,l,r,x); int mid = (l + r)>>;
if (L <= mid)
{
update(val,L,R,l,mid,x<<);
}
if(R > mid)
{
update(val,L,R,mid+,r,x<<|);
}
PushUp(x);
} int n,m,ans; void query(int l,int r,int x)
{
if(T[x].l == l && T[x].r == r)
{
ans += T[x].c;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
query(l,r,(x<<)+);
}
else if(r<=mid)
{
query(l,r,(x<<));
}
else
{
query(l,mid,(x<<));
query(mid+,r,(x<<)+);
}
} int a[MAXN]; int main()
{
int t,i,kase=;
sf("%d",&t);
while(t--)
{
sf("%d",&n);
build(,n,);
sf("%d",&m);
for(i=;i<=m;i++)
{
int x,y,z;
sf("%d%d%d",&x,&y,&z);
update(z,x,y,,n,);
}
pf("Case %d: The total value of the hook is %d.\n",kase++,T[].c);
}
return ;
}
区间增减，区间求和
模板：
struct node
{
LL l,r,c,f;
}T[MAXN<<]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
//pf("%d %d\n",rt,T[rt].c);
} void PushDown(int rt,int m)
{
if(T[rt].f)
{
T[rt<<].f += T[rt].f;
T[(rt<<) + ].f += T[rt].f;
T[rt<<].c += T[rt].f * (m-(m>>));
T[(rt<<)+].c += T[rt].f * (m>>);
T[rt].f = ;
}
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].f = ;
T[x].c = ;
if(l==r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
T[x].f += val;
T[x].c += val*(r-l+);
//pf("%d %d %d\n",T[x].c,l,r);
return;
}
PushDown(x,r-l+);
//pf("%d %d %d %d %d %d\n",val,L,R,l,r,x); int mid = (l + r)>>;
if (L <= mid)
{
update(val,L,R,l,mid,x<<);
}
if(R > mid)
{
update(val,L,R,mid+,r,x<<|);
}
PushUp(x);
} LL ans; int n,m; void query(int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
ans += T[x].c;
return;
}
PushDown(x,r-l+);
int mid = (l + r)>>;
if(L <= mid) query(L,R,l,mid,x<<);
if(R > mid) query(L,R,mid+,r,x<<|);
PushUp(x);
}
poj 3468
#include <iostream>
#include <string>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <stack>
#include <queue>
#include <cctype>
#include <vector>
#include <iterator>
#include <set>
#include <map>
#include <sstream>
using namespace std; #define mem(a,b) memset(a,b,sizeof(a))
#define pf printf
#define sf scanf
#define spf sprintf
#define pb push_back
#define debug printf("!\n")
#define MAXN 111111 + 5
#define MAX(a,b) a>b?a:b
#define blank pf("\n")
#define LL long long
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define pqueue priority_queue
#define INF 0x3f3f3f3f struct node
{
LL l,r,c,f;
}T[MAXN<<]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
//pf("%d %d\n",rt,T[rt].c);
} void PushDown(int rt,int m)
{
if(T[rt].f)
{
T[rt<<].f += T[rt].f;
T[(rt<<) + ].f += T[rt].f;
T[rt<<].c += T[rt].f * (m-(m>>));
T[(rt<<)+].c += T[rt].f * (m>>);
T[rt].f = ;
}
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].f = ;
if(l==r)
{
scanf("%I64d",&T[x].c);
return;
}
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
PushUp(x);
} void update(int val,int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
T[x].f += val;
T[x].c += val*(r-l+);
//pf("%d %d %d\n",T[x].c,l,r);
return;
}
PushDown(x,r-l+);
//pf("%d %d %d %d %d %d\n",val,L,R,l,r,x); int mid = (l + r)>>;
if (L <= mid)
{
update(val,L,R,l,mid,x<<);
}
if(R > mid)
{
update(val,L,R,mid+,r,x<<|);
}
PushUp(x);
} LL ans; int n,m; void query(int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
ans += T[x].c;
return;
}
PushDown(x,r-l+);
int mid = (l + r)>>;
if(L <= mid) query(L,R,l,mid,x<<);
if(R > mid) query(L,R,mid+,r,x<<|);
} int main()
{
int t,i,kase=;
while(~sf("%d%d",&n,&m))
{
build(,n,);
/*
for(i=1;i<=n;i++)
{
int tmp;
sf("%d",&tmp);
update(tmp,i,i,1,n,1);
}
*/
for(i=;i<=m;i++)
{
int x,y,z;
char s[];
sf("%s",s);
if(s[]=='Q')
{
ans = ;
sf("%d%d",&x,&y);
query(x,y,,n,);
pf("%I64d\n",ans);
}
else
{
sf("%d%d%d",&x,&y,&z);
update(z,x,y,,n,);
}
}
}
return ;
}
ACM-线段树的更多相关文章
- hdu acm 1166 敌兵布阵 （线段树）
敌兵布阵 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submi ...
- 【ACM】hud1166 敌兵布阵（线段树）
经验: cout 特别慢 如果要求速度 全部用 printf !!! 在学习线段树 内容来自:http://www.cnblogs.com/shuaiwhu/archive/2012/04/22/24 ...
- ACM: Billboard 解题报告-线段树
Billboard Time Limit:8000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Descript ...
- HDU 4911 http://acm.hdu.edu.cn/showproblem.php?pid=4911(线段树求逆序对）
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4911 解题报告: 给出一个长度为n的序列,然后给出一个k,要你求最多做k次相邻的数字交换后,逆序数最少 ...
- HDU 5029 Relief grain（离线+线段树+启发式合并）（2014 ACM/ICPC Asia Regional Guangzhou Online）
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5029 Problem Description The soil is cracking up beca ...
- HDU 4031 Attack（离线+线段树）（The 36th ACM/ICPC Asia Regional Chengdu Site —— Online Contest）
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4031 Problem Description Today is the 10th Annual of ...
- UPC 2224 Boring Counting ★(山东省第四届ACM程序设计竞赛 tag:线段树)
[题意]给定一个长度为N的数列,M个询问区间[L,R]内大于等于A小于等于B的数的个数. [题目链接]http://acm.upc.edu.cn/problem.php?id=2224 省赛的时候脑抽 ...
- 【线段树】HDU 5493 Queue (2015 ACM/ICPC Asia Regional Hefei Online)
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=5493 题目大意: N个人,每个人有一个唯一的高度h,还有一个排名r,表示它前面或后面比它高的人的个数 ...
- 2018牛客网暑假ACM多校训练赛（第七场）I Tree Subset Diameter 动态规划 长链剖分 线段树
原文链接https://www.cnblogs.com/zhouzhendong/p/NowCoder-2018-Summer-Round7-I.html 题目传送门 - https://www.n ...
- 2018牛客网暑假ACM多校训练赛（第六场）I Team Rocket 线段树
原文链接https://www.cnblogs.com/zhouzhendong/p/NowCoder-2018-Summer-Round6-I.html 题目传送门 - https://www.no ...
随机推荐
- 2. C语言文件操作经典习题
1. 统计英文文本文件中,有多少个大写字母.小写字母.数字.空格.换行以及其他字符. #define _CRT_SECURE_NO_WARNINGS #include <stdio.h> ...
- promise思考
我写了三个单元块,分别对应三种业务场景 let query;query = (url) => { url=url||"传递的参数为空"; return new Promise ...
- SDUT OJ 数据结构实验之串三：KMP应用
数据结构实验之串三:KMP应用 Time Limit: 1000 ms Memory Limit: 65536 KiB Submit Statistic Discuss Problem Descrip ...
- IO模型之三Reactor 和 Proactor IO设计模式
反应器Reactor: 在事件驱动的应用中,应用中的请求总是通过事件(如CONNECTOR.READ.WRITE等)来表示,当多个请求同时到来时,这些请求最终还是会被序列化地处理,在序列化处理这些服务 ...
- rabbitmq生产者代码,以及过程参数含义:
首先pom依赖: <?xml version="1.0" encoding="UTF-8"?> <project xmlns="ht ...
- Qt 学习之路 2（53）：自定义拖放数据
Qt 学习之路 2(53):自定义拖放数据 豆子 2013年5月26日 Qt 学习之路 2 13条评论上一章中,我们的例子使用系统提供的拖放对象QMimeData进行拖放数据的存储.比如使用QM ...
- struts2学习笔记（三）—— struts2的常见配置
一.配置文件的加载顺序 每次从客户端发送请求到服务器都要先经过Struts2的核心过滤器StrutsPrepareAndExecuteFilter,这个过滤器有两个功能:预处理和执行.在预处理中主要就 ...
- C++_标准模板库STL概念介绍4-算法
STL包含很多处理容器的非成员函数: sort() copy() find() random_shuffle() set_union() set_intersection() set_differen ...
- UVALive - 7061 区间DP初步
题意:杀一只狼i会收到a[i]+b[i当前左边]+b[i当前右边]的攻击,求杀死所有狼的最小代价 #include<iostream> #include<algorithm> ...
- 云服务的三种形式laas,paas,saas
“云”其实是互联网的一个隐喻,“云计算”其实就是使用互联网来接入存储或者运行在远程服务器端的应用,数据,或者服务. 云也是分层的 任何一个在互联网上提供其服务的公司都可以叫做云计算公司.其实云计算分几 ...