曼哈顿距离、欧几里得距离、闵氏距离(p→∞为切比雪夫距离)

曼哈顿距离:

是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即d（i，j）=|xi-xj|+|yi-yj|。

对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。

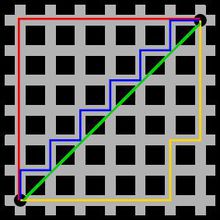
欧几里得距离:

欧几里得度量（euclidean metric）（也称欧氏距离）是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。

计算公式

欧几里得度量二维空间的公式

0ρ = sqrt( (x1-x2)^2+(y1-y2)^2 )　|x| = √( x2 + y2 )

欧几里得度量三维空间的公式

0ρ = √( (x1-x2)^2+(y1-y2)^2+(z1-z2)^2 )　|x| = √( x2 + y2 + z2 )

欧几里得度量n维空间的公式

n维欧氏空间是一个点集,它的每个点 X 或向量 x 可以表示为 (x[1]，x[2]，…，x[n]) ，其中 x[i](i = 1，2，…，n) 是实数，称为 X 的第i个坐标。

两个点 A = (a[1]，a[2]，…，a[n]) 和 B = (b[1]，b[2]，…，b[n]) 之间的距离 ρ(A，B) 定义为下面的公式：

ρ(A，B) =√ [ ∑( a[i] - b[i] )^2 ] (i = 1，2，…，n)

向量 x = (x[1]，x[2]，…，x[n]) 的自然长度 |x| 定义为下面的公式：

|x| = √( x[1]^2 + x[2]^2 + … + x[n]^2 )

 

 

闵氏距离:

又叫做闵可夫斯基距离,是欧氏空间中的一种测度，被看做是欧氏距离的一种推广，欧氏距离是闵可夫斯基距离的一种特殊情况。

定义式：ρ(A，B) = [ ∑( a[i] - b[i] )^p ]^(1/p) (i = 1，2，…，n)

闵可夫斯基距离公式中，当p=2时，即为欧氏距离；当p=1时，即为曼哈顿距离；当p→∞时，即为切比雪夫距离。