【洛谷 P1363】幻想迷宫（搜索）

这题其实可以很简单。

题目叫做“幻想迷宫”，那么我们就幻想一个迷宫。

借用一下@FancyDreams的图片

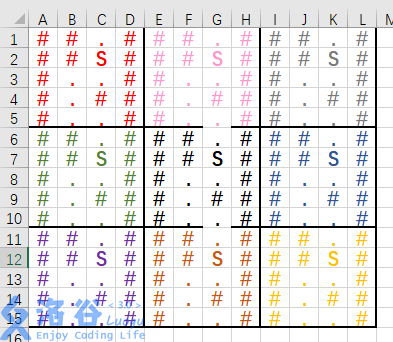
只有左上角第一个\(5*4\)的迷宫是真的,

其他都是我们幻想出来的。

并且，我们幻想自己在中间那个\(5*4\)的迷宫里的S处，我们并不需要开多很多倍的数组，要获取这个位置是'.'还是'#'，只需对当前坐标取余\(n,m\)即可。注意一个细节，直接取余的话若\(x=n\)，那么取余后就变成0了，所以我们要这样：

\[(x-1)\ mod\ n + 1
\]

y坐标同理。每走到一个点标记vis[取模后的坐标] = 当前迷宫的坐标，比如上图中，左上角的迷宫坐标是1，中上那个是2，最中间的是5，右下角的是9。

然后向4个方向拓展，如果这里不是'#'，再判断，如果这个位置走过了并且不是在当前幻想的迷宫走的，那么恭喜，\(flag = 1; return;\)。否则继续搜。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#define rep(i,m,n) for(int i=m;i<=n;++i)
#define dop(i,m,n) for(int i=m;i>=n;--i)
using namespace std;
inline int read(){
    int s = 0, w = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-')w = -1;if(ch==-1) exit(0); ch = getchar();} //快读小细节，getchar()==-1时直接exit(0);
    while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0',ch = getchar();
    return s * w;
}
const int MAXN = 1600;
char a[MAXN][MAXN];
int n, m, sx, sy;
int vis[MAXN][MAXN], flag;
int l[] = { 233, -1, 1, 0, 0 }, r[] = { 666, 0, 0, -1, 1 };
inline char get(int x, int y){//获取当前的位置能不能走
    return a[(x - 1) % n + 1][(y - 1) % m + 1];
}
void dfs(int x, int y){
    if(flag) return; //找到了，直接返回
    vis[(x - 1) % n + 1][(y - 1) % m + 1] = ((x / n - !(x % n)) * 3 + (y / m - !(y % m)) + 1); //标记这个位置是在当前幻想的迷宫走的
    rep(i, 1, 4){ //向四个方向拓展
       int X = x + l[i], Y = y + r[i];//X,Y为要到的位置
       if(vis[(X - 1) % n + 1][(Y - 1) % m + 1] && vis[(X - 1) % n + 1][(Y - 1) % m + 1] != ((X / n - !(X % n)) * 3 + (Y / m - !(Y % m)) + 1)){ //如果走过了并且不是在当前迷宫走的，说明可以重复到达这个位置，也就是可以无限的走
         flag = 1;
         return ;
       }
       if(get(X, Y) != '#' && !vis[(X - 1) % n + 1][(Y - 1) % m + 1]) dfs(X, Y); //如果能走，dfs
    }
}
int main(){
    while(233){
      n = read(); m = read();
      rep(i, 1, n) rep(j, 1, m){
         a[i][j] = getchar();
         while(a[i][j] != '.' && a[i][j] != '#' && a[i][j] != 'S')
           a[i][j] = getchar();
         if(a[i][j] == 'S') sx = i, sy = j;
      }
      dfs(sx + n * 100, sy + m * 100);
      memset(vis, 0, sizeof(vis));
      if(flag){
        printf("Yes\n");
        flag = 0;
      }
      else printf("No\n");
    }
    return 0;
}