【BZOJ1419】 Red is good [期望DP]

Red is good

Time Limit: 10 Sec  Memory Limit: 64 MB
[Submit][Status][Discuss]

Description

　　桌面上有R张红牌和B张黑牌，随机打乱顺序后放在桌面上，开始一张一张地翻牌，翻到红牌得到1美元，黑牌则付出1美元。可以随时停止翻牌，在最优策略下平均能得到多少钱。

Input

　　一行输入两个数R,B。

Output

　　在最优策略下平均能得到多少钱。输出答案时,小数点后第六位后的全部去掉,不要四舍五入。

Sample Input

　　5 1

Sample Output

　　4.166666

HINT

　　R,B<=5000

Solution

　　这显然是一道简单的期望DP。我们令 f[i][j] 表示剩下 i 个红牌和 j 个黑牌时的最优答案。那么显然：

　　

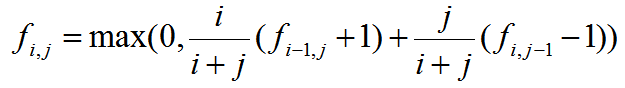
　　其中 i/(i+j) 和 j/(i+j) 表示选择到的概率。

　　最后由于卡内存，我们滚动一下数组即可。

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;
 typedef long long s64; 

 const int ONE = ;
 const int E6 = 1e6;

 int n,m;
 double f[][];

 int get()
 {
         int res=,Q=;  char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 int main()
 {
         n=get();    m=get();
         for(int i=,A=; i<=n; i++,A^=)
         {
             f[A][] = i;
             for(int j=; j<=m; j++)
                 f[A][j] = max(0.0, (double)i/(i+j) * (f[A^][j]+) + (double)j/(i+j) * (f[A][j-]-) );
         }
         s64 record = floor(f[n&][m] * E6);
         printf("%lld.%06lld", record/E6, record%E6);
 }