[TJOI2007]segment

题目描述

在一个 n*n 的平面上，在每一行中有一条线段，第 i 行的线段的左端点是(i, L(i))，右端点是(i, R(i))，其中 1 ≤ L(i) ≤ R(i) ≤ n。

你从(1, 1)点出发，要求沿途走过所有的线段，最终到达(n, n)点，且所走的路程长度要尽量短。

更具体一些说，你在任何时候只能选择向下走一步（行数增加 1）、向左走一步（列数减少 1）或是向右走一步（列数增加 1）。当然，由于你不能向上行走，因此在从任何一行向下走到另一行的时候，你必须保证已经走完本行的那条线段。

输入输出格式

输入格式：

输入文件的第一行有一个整数 n，以下 n 行，在第 i 行（总第(i+1)行）的两个整数表示L(i)和 R(i)。

输出格式：

输出文件仅包含一个整数，你选择的最短路程的长度。

输入输出样例

输入样例#1：

6

2 6

3 4

1 3

1 2

3 6

4 5

输出样例#1：

24

说明

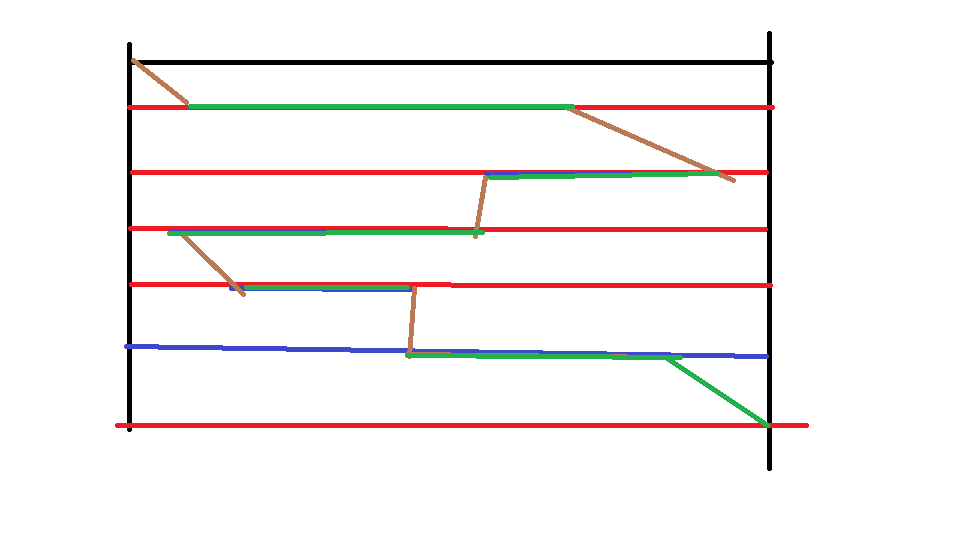
我们选择的路线是

(1,1) (1,6)

(2,6) (2, 3)

(3, 3) (3, 1)

(4, 1) (4, 2)

(5, 2) (5, 6)

(6, 6) (6, 4) (6, 6)

不难计算得到，路程的总长度是 24。 100%的数据中，n ≤ 20 000。

一眼看上去是一个dp题

对于这个题目

在一行中

我们要么从左至右走完这行的线段

要么从右至左走完这行的线段

所以转移方程就很好写了

#include<iostream>
#include<cstdlib>
#include<cstdio>
#define N 20005
using namespace std;

struct line{
    int l,r,len;
}q[N];

int f[N][5],n,ans;

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d%d",&q[i].l,&q[i].r);
        q[i].len=q[i].r-q[i].l;
    }
    f[1][1]=q[1].l-1;
    f[1][3]=q[1].r-1;
    f[1][2]=q[1].len+f[1][3];
    f[1][4]=q[1].len+f[1][1];
    for(i=2;i<=n;i++){
        f[i][1]=min(f[i-1][2]+abs(q[i-1].l-q[i].l)+1,f[i-1][4]+abs(q[i-1].r-q[i].l)+1);
        f[i][3]=min(f[i-1][2]+abs(q[i-1].l-q[i].r)+1,f[i-1][4]+abs(q[i-1].r-q[i].r)+1);
        f[i][2]=f[i][3]+q[i].len;
        f[i][4]=f[i][1]+q[i].len;
    }
    ans=min(n-q[n].l+f[n][2],n-q[n].r+f[n][4]);
    printf("%d\n",ans);
    return 0;
}