数学图形之SineSurface与粽子曲面

SineSurface直译为正弦曲面.这有可能和你想象的正弦曲线不一样.如果把正弦曲线绕Y轴旋转,得到的该是正弦波曲面.这个曲面与上一节中的罗马曲面有些相似,那个是被捏过的正四面体,这个则是个被捏过正方体.

本文将展示SineSurface与粽子曲面的生成算法和切图,使用自己定义语法的脚本代码生成数学图形.相关软件参见:数学图形可视化工具,该软件免费开源.QQ交流群: 367752815

这是从http://mathworld.wolfram.com/SineSurface.html上找到的一种曲面.

其曲面的参数方程如下:

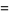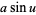			(1)
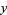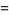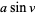			(2)
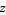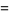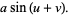			(3)

It is a sextic surface with algebraic equation (sextic是"六次的"意思, 一开始我还以为是"性感的"意思)

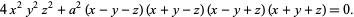从它的参数方程公式来看,就知道它为什么叫正弦曲面了.

脚本代码:

#http://mathworld.wolfram.com/SineSurface.html

vertices = D1: D2:

u = from  to (PI*) D1
v = from  to (PI*) D2

x = sin(u)
y = sin(v)
z = sin(u + v)

a = 

x = x*a
y = y*a
z = z*a

如果将脚本中的正弦函数改为余弦函数,那么会得到粽子曲面.

粽子曲面这个名子是我取的,因为它就像个粽子.

vertices = D1: D2:

u = from  to (PI*) D1
v = from  to (PI*) D2

x = cos(u)
y = cos(v)
z = cos(u + v)

a = 

x = x*a
y = y*a
z = z*a