[网络流24题] 最长k可重区间集

https://www.luogu.org/problemnew/show/3358

以区间(1,5),(2,6),(7,8)为例

建模方法一：

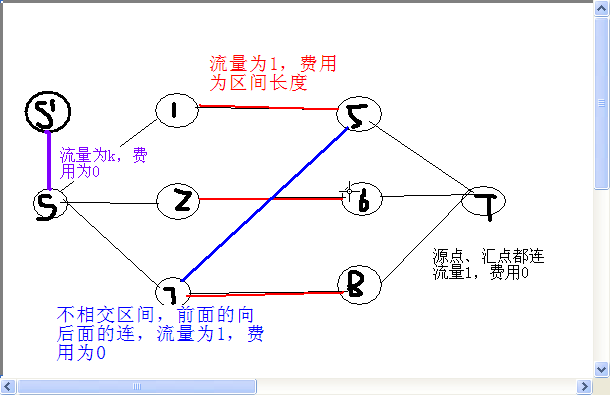
建模方法二：

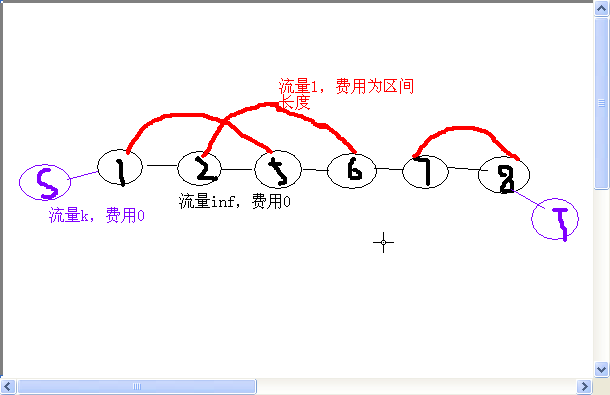
离散化区间端点

相当于找k条费用最大的不相交路径

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;

#define N 1011
#define M 3011

typedef long long LL;

int h[N];

struct node
{
    int l,r;
}e[];

int src,decc;

int front[N],to[M<<],nxt[M<<],from[M<<],cnt=;
int cap[M<<];
LL cost[M<<];

LL dis[N];
int path[N];

bool vis[N];

void read(int &x)
{
    x=; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar(); }
}

void add(int u,int v,int w,int val)
{
    to[++cnt]=v; nxt[cnt]=front[u]; front[u]=cnt; from[cnt]=u; cap[cnt]=w; cost[cnt]=val;
    to[++cnt]=u; nxt[cnt]=front[v]; front[v]=cnt; from[cnt]=v; cap[cnt]=; cost[cnt]=-val;
}

bool spfa()
{
    queue<int>q;
    memset(dis,,sizeof(dis));
    dis[src]=;
    vis[src]=true;
    q.push(src);
    int now;
    while(!q.empty())
    {
        now=q.front();
        q.pop();
        vis[now]=false;
        for(int i=front[now];i;i=nxt[i])
        {
            if(cap[i]> && dis[to[i]]<dis[now]+cost[i])
            {
                dis[to[i]]=dis[now]+cost[i];
                path[to[i]]=i;
                if(!vis[to[i]])
                {
                    q.push(to[i]);
                    vis[to[i]]=true;
                }
            }
        }
    }
    return dis[decc]>;
}

int main()
{
    freopen("interv.in","r",stdin);
    freopen("interv.out","w",stdout);
    int n,k;
    read(n);
    read(k);
    int tot=;
    for(int i=;i<=n;++i)
    {
        read(e[i].l);
        read(e[i].r);
        if(e[i].l>e[i].r) swap(e[i].l,e[i].r);
        h[++tot]=e[i].l;
        h[++tot]=e[i].r;
    }
    sort(h+,h+tot+);
    tot=unique(h+,h+tot+)-h-;
    for(int i=;i<=n;++i)
    {
        e[i].l=lower_bound(h+,h+tot+,e[i].l)-h;
        e[i].r=lower_bound(h+,h+tot+,e[i].r)-h;
    }
    for(int i=;i<tot;++i) add(i,i+,1e9,);
    decc=tot+;
    add(src,,k,);
    add(tot,decc,k,);
    for(int i=;i<=n;++i) add(e[i].l,e[i].r,,h[e[i].r]-h[e[i].l]);
    LL ans=;
    int now,j;
    while(spfa())
    {
        ans+=dis[decc];
        now=decc;
        while(now!=src)
        {
            j=path[now];
            cap[j]--;
            cap[j^]++;
            now=from[path[now]];
        }
    }
    cout<<ans;
}

题目描述

对于给定的开区间集合 I 和正整数 k，计算开区间集合 I 的最长 k可重区间集的长度。

输入输出格式

输入格式：

的第 1 行有 2 个正整数 n和 k，分别表示开区间的个数和开区间的可重迭数。接下来的 n行，每行有 2 个整数，表示开区间的左右端点坐标。

输出格式：

将计算出的最长 k可重区间集的长度输出

输入输出样例

输入样例#1： 复制

4 2
1 7
6 8
7 10
9 13 

输出样例#1： 复制

15

说明

对于100%的数据，1\le n\le 5001≤n≤500,1\le k\le 31≤k≤3