【洛谷P1069 细胞分裂】

题目链接

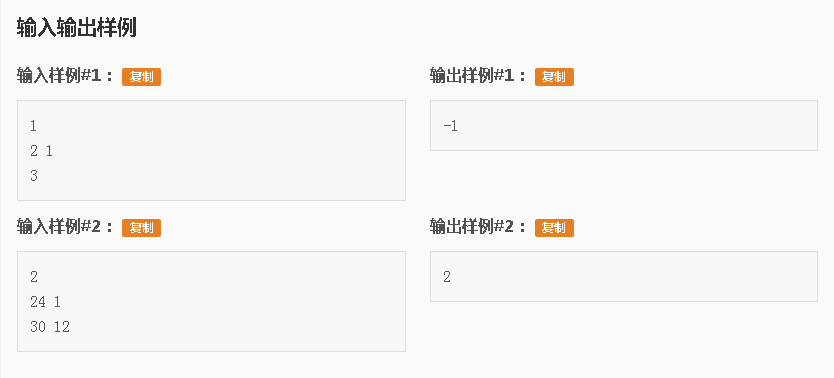
首先，光看题就觉得它很扯淡（你哪里来这么多的钱来买试管）

根据某位已经ak过ioi的名为ych的神仙说（一看就是数学题，一看就需要因式分解，emm，我果然没有发现美的眼睛qwq）

那么我们就根据ych神仙的思路找到了通往AC的道路

代码摘自（神仙的考试程序qwq）

#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<iomanip>
#include<cmath>
#include<cstring>
#include<string>
#include<algorithm>
#include<time.h>
#include<queue>
#include<stack>
using namespace std;
inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}
//首先这道题显然是道数学题(要不然这数据怎么玩)
//样例1的解释启发我们这道题可以通过分解质因数做
//这个题其实条件等价于求a^x=k(m1^m2)的最小x值
//我们可以对两边进行分解质因数
//发现如果方程有解，则m1中不能包含a中没有的质因子
//但是a1的质因子可以比m1多
//那么最小的x就是找到最大的次数差值
struct prime
{
    int cnt,pn[],t[];
}p,q;//一个储存题目给的条件,一个储存判断
int n,m1,m2;
inline void fenjie(int t,prime& p)//质因数分解2
{
    p.cnt=;
    for(int i=;i*i<=t;++i)
    {
        if(!(t%i))
        {
            p.pn[++p.cnt]=i;//记录第cnt个约数
            p.t[p.cnt]=;
            do
            {
                t/=i;
                ++p.t[p.cnt];//次数
            }while(!(t%i));
        }
    }
    if(t>)
    {
        p.pn[++p.cnt]=t;
        p.t[p.cnt]=;
    }
}
int main()
{
    freopen("cell.in","r",stdin);
     freopen("cell.out","w",stdout);
    n=read(),m1=read(),m2=read();
    if(m1==) return cout<<<<endl,;//先判断一波特殊情况
    fenjie(m1,p);//把m1分解,存到p里
    int ans,x;
    ans=-;
    for(int i=;i<=n;i++)
    {
        x=read();
        fenjie(x,q);
        int maxn=,nxt=;
        //我们用nxt来存储x的下一个质因子的序号
        bool flag=false;
        if(q.cnt>=p.cnt)
        //只有要求判断的数的质因子的个数>=题目给的条件的质因子的个数才能继续
        for(int j=;j<=p.cnt;j++)//枚举m1的每一个质因子
        {
            while(q.pn[nxt]<p.pn[j]&&nxt<=q.cnt)++nxt;
            if(nxt>q.cnt||q.pn[nxt]>p.pn[j])break;//如果没有这个质因子就跳出
            int f=p.t[j]*m2/q.t[nxt];
            if((p.t[j]*m2)%(q.t[nxt])) f++;
            //让这两个次数相等,因为有可能不整除，所以还要判断一下，相当于向上取整
            if(maxn<f)maxn=f;//求最大值
            if(j==p.cnt) flag=; //标记答案
            else flag=;
        }
        if(flag&&(ans==-||ans>maxn))ans=maxn;
    }
    printf("%d\n",ans);
    return ;
}