密码学之RSA基础

预备数论知识

互质关系

如果两个正整数，除了1以外，没有其他公因子，那么就称这两个数是互质关系

比如：4和7，13和61

欧拉函数

思考：任意给定整数n，在小于等于n的正整数中，有多少个数与n构成互质关系？

计算这个值的方法即欧拉函数，以$φ(n)$表示

第一种情况：

如果n=1，则$φ(n)$=1,因为1和任何数互质

第二种情况：

如果n是质数，则$φ(n)$=n-1；易证

第三种情况：

如果n是质数的某一次方，即：$$n=p^k \quad(p为质数，k为大于1的整数)$$

则：$$φ(p^k)=pk-p^{k-1}=pk(1-\frac{1}{p})$$

因为只有当一个数的公因数中不包含质数p，才可能与n互质，而包含质数p的数一共有$p^{k-1}$个

第四种情况：

如果n可以分解为两个质数的整数之积，即：$$n=p_1 * p_2$$

则：$$φ(n)=φ(p_1p_2)=φ(p_1^k)φ(p_2k)$$

第五种情况：

任意一个大于1的整数都能够因式分解为一系列质数的乘积：$$n=p_1^{k1}p_2{k2}···p_m^{km}$$

即：$$φ(n)=φ(p_1^{k1})φ(p_2{k2})···φ(p_m^{km}) $$

即：$$φ(n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})···(1-\frac{1}{p_m})$$

欧拉定理

如果两个正整数a和n互质，则n的欧拉函数$φ(n)$可以使得下面的等式成立：

\[a^{φ(n)}\equiv1(mod \quad n)
\]

也就是说，a的$φ(n)$次方被n除的余数为1。或者说，a的$φ(n)$次方减去1，可以被n整除。

假设正整数a与质数p互质，因为质数p的$φ(p)$等于p-1，则欧拉定理可以写成

\[a^{p-1}\equiv1(mod \quad n)
\]

模反元素

如果两个正整数a和n互质，那么一定可以找到整数b，使得 a*b-1 被n整除，或者说a*b被n除的余数是1。

\[a*b\equiv1(mod \quad n)
\]

这个时候b称之为a的模反元素

RSA算法

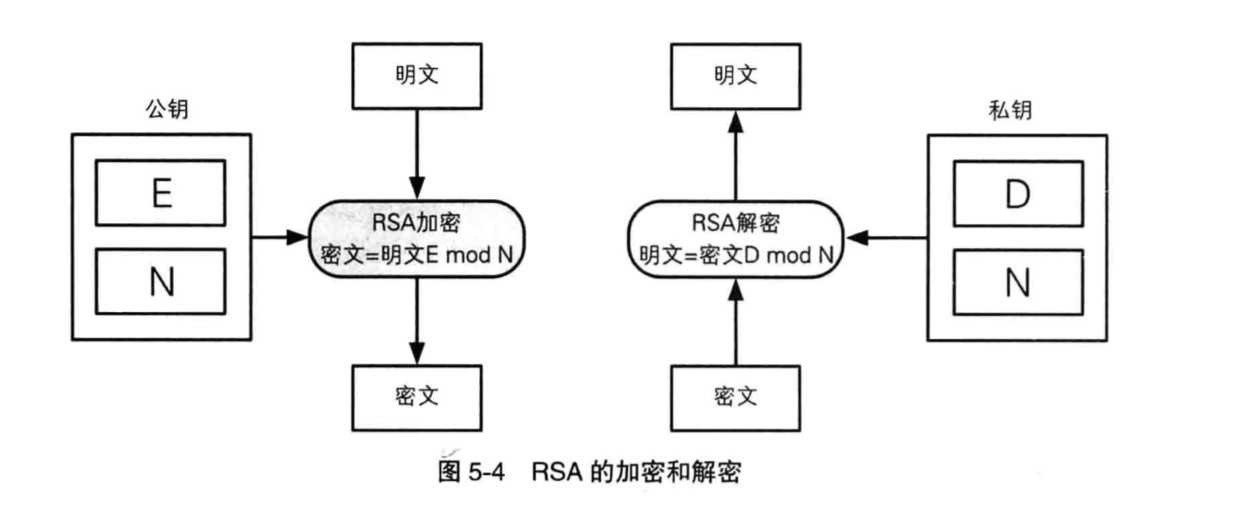
RSA是一种公钥密码算法，简单来说就是：

加密：

密文=明文^E mod N

也就是说RSA的密文是代表明文的数字的E次方求mod N得结果

解密：

明文=密文^D mod N

对密文得数字得D次方求mod N就可以得到明文

例：现在Alice要向Bob发送信息

选择两个质数p=63，q=71
计算n=p*q=4473
计算L=lcm(p-1,q-1)，L是（p-1）和（q-1）的最小公倍数，所以求得L=2170
选择一个随机整数$e (1<e<L)$，并且$e和L互质$，也就是要找出满足gcd(e,L)=1得数e，也就是e和L的最大公约数为1，可以使用伪随机生成器，通过伪随机生成器在1<e<L得范围内生成e得侯选数，然后判断是否满足gcd(e,L)=1，求最大公约数可以使用欧几里得的辗转相除法。

这里选e=13
计算$e对L的模反元素d$，即$e*d \equiv1(mod \quad L)$

即：$e*d-1=k·L$
解方程：$13x-2170y=1$，其中x和y为整数

def ext_euclid(a,b):

	d=b//a+1

	while(d>0):

		if (a*d-1)%b==0:

			k=(a*d-1)//b

			print("d=%d,k=%d"%(d,k))

			d=0

		else:

			d+=1

if __name__ == '__main__':

	ext_euclid(13,2170)

最后求得：(167, 1），所以得到d=167，k=1

将（e,n）和（d,n）封装成公钥和私钥，即公钥（13，4473）和私钥（167，4473）
明文：m（m<n，且为整数），这里假设m=55，密文为c

\[m^e\equiv c( mod \quad n)
\]

即55的13次方除以4473的余数等于c，：

\[55^{13}\equiv c(mod \quad4473)
\]

得到：c=3331

解密信息

\[c^d \equiv m(mod\quad n)
\]

即m等于3331的2003次方除以4473的余数：

\[3331^{167} \equiv m(mod \quad 4473)
\]

求得：m=55

对RSA的攻击

破译者能够获取的信息：密文（m）、公钥（e，n）

破译者不知道的信息：明文（c）、私钥中的（d）、q、p、L

解密过程如下，也就是说我们只要嫩巩固获得D，那么就能破译密文了

明文=密文^D mod N

暴力破解获得 D

在有限的时间和有限的计算能力下，只要D的长度在安全范围内，难以实现；

通过`e`和`n`求出D

e*D mod L=1

要想获得D的值，就得知道L的值是多少

L=lcm(p-1,q-1)

然后得知道p和q的值

N=p*q

所以只要能够对N进行因数分解求出p和q，也就能够破译密文了

而目前还未能够有发现对大整数进行质数因数分解的高效算法，目前已知能够分解的最大长度为768位。

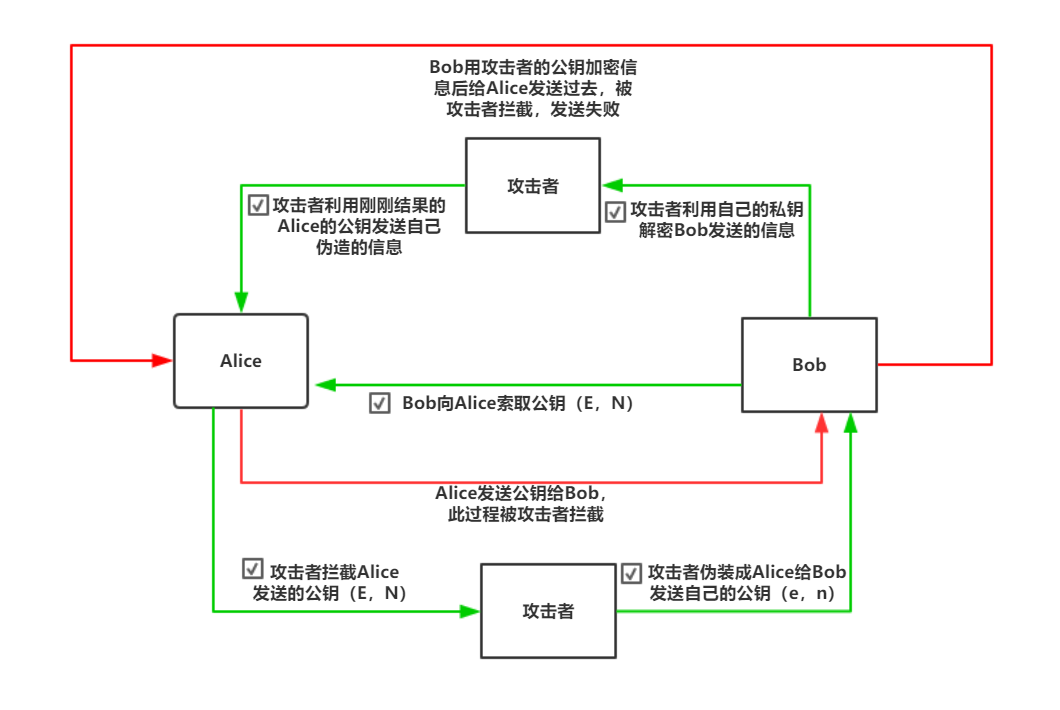
中间人攻击

中间人攻击就是主动攻击者混入真正的发送者和接收者之间，对发送者伪装成接收者，对接收者伪装成发送者。

参考：

《图解密码技术》：https://item.jd.com/11942019.html

阮一峰的网络日志：http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html