迁移学习（CDAN）《Conditional Adversarial Domain Adaptation》（已复现迁移）

论文信息

论文标题：Conditional Adversarial Domain Adaptation
论文作者：Yaroslav Ganin, Evgeniya Ustinova, Hana Ajakan, Pascal Germain
论文来源：JMLR 2016
论文地址：download 
论文代码：download
引用次数：5292

1 背景

1. 1 问题

• 普通的对抗域自适应方法仅独立对齐特征，而未对于标签进行对齐，往往不充分 ==============> 对齐特征与类别的联合分布
• 当数据分布包含复杂的多模态结构时，对抗性自适应方法可能无法捕捉到这样的多模态结构，多模态结构只能通过特征和类之间的交叉协方差依赖性来充分捕获；即使判别器完全混淆，也不能保证两个分布完全相似 ==============> 多线性调整
• 条件域判别器强制使不同的样本具有相同的重要性，可能导致不确定预测的难迁移样本也许会对抗适应产生不良影响 ==============> 熵调整

1.2 条件生成对抗网络(CGAN)

　　

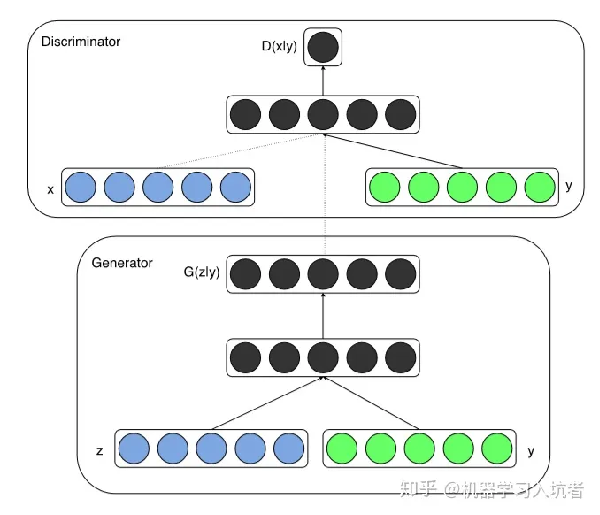
• CGAN 是在 GAN 基础上做的一种改进，通过给原始 GAN 的生成器和判别器添加额外的条件信息（类别标签或者其它辅助信息），实现条件生成模型
• 对于生成器将类别标签与噪声信号的组合作为生成图片的输入；对于判别器将类别标签与图像数据拼接结果 x⨁y 作为输入
• CGAN 可解决带标签的数据生成问题

2 方法

2.1 整体框架(CDAN)

　　

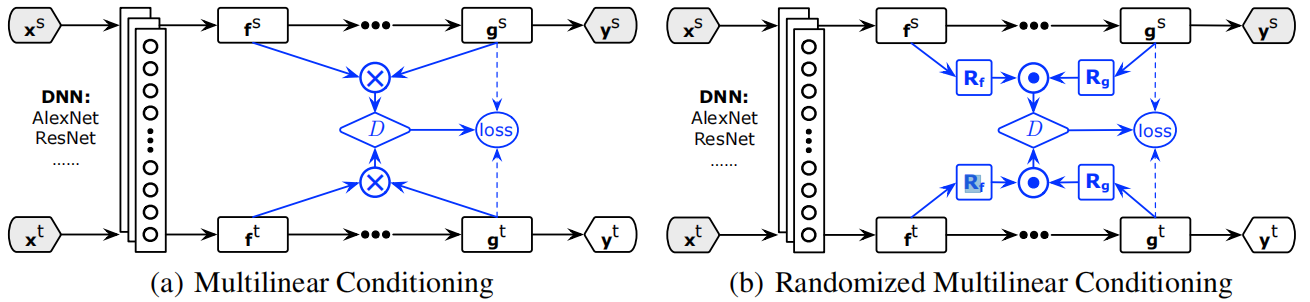
　　(a) 多线性调整：适用于低维场景, 将特征与类别的多线性映射 $T_{\otimes}(f, g)$ 作为鉴别器 $D$ 的输入
　　(b) 随机多线性调整：适用于高维场景, 随机抽取 $f$, $g$  上的某些维度的多线性映射 $T_{\odot}(f, g)$  作为鉴别器的输入损失函数

　　损失函数：

　　　　$\begin{array}{l}\mathcal{E}(G)=\mathbb{E}_{\left(\mathbf{x}_{i}^{s}, \mathbf{y}_{i}^{s}\right) \sim \mathcal{D}_{s}} L\left(G\left(\mathbf{x}_{i}^{s}\right), \mathbf{y}_{i}^{s}\right) \\\mathcal{E}(D, G)=-\mathbb{E}_{\mathbf{x}_{i}^{s} \sim \mathcal{D}_{s}} \log \left[D\left(\mathbf{f}_{i}^{s}, \mathbf{g}_{i}^{s}\right)\right]-\mathbb{E}_{\mathbf{x}_{j}^{t} \sim \mathcal{D}_{t}} \log \left[1-D\left(\mathbf{f}_{j}^{t}, \mathbf{g}_{j}^{t}\right)\right] \\ \underset{G}{\text{min}}   \quad \mathcal{E}(G)-\lambda \mathcal{E}(D, G) \\  \underset{D}{\text{min}}  \quad \mathcal{E}(D, G) \end{array}$

2.2 $f \oplus g$ 与 $f \otimes g$

　　$f \oplus g$  串联: 直接将特征表示和分类器预测的类别标签拼接起来，由于 $f$, $g$  相互独立，无法完全捕获特征表示和分类器预测之间的乘法交互作用，均值映射独立计算 $x$, $y$ 的均值：

　　　　$\mathbb{E}_{\mathbf{x y}}[\mathbf{x} \oplus \mathbf{y}]=\mathbb{E}_{\mathbf{x}}[\mathbf{x}] \oplus \mathbb{E}_{\mathbf{y}}[\mathbf{y}]$

　　即：将类信息和特征信息简单拼接；　　

　　$f \otimes g$  多线性映射：模拟了不同变量之间的乘法相互作用，可以完全捕捉复杂数据分布背后的多模态结构，均值映射计算了每个类条件分布 $P(x \mid y)$  的 均值:

　　$\mathbb{E}_{\mathbf{x y}}[\mathbf{x} \otimes \mathbf{y}]=\mathbb{E}_{\mathbf{x}}[\mathbf{x} \mid y=1] \oplus \ldots \oplus \mathbb{E}_{\mathbf{x}}[\mathbf{x} \mid y=C]$

　　即：用类信息对每个样本特征加权，然后拼接；

2.3 梯度爆炸

　　多线性映射的维度为 $f$, $g$ 的维度之积，易导致维度爆炸， 因此采用随机方法解决此问题，抽取 $f$, $g$ 上的某些维度做多线性映射，以近似 $f \otimes g$ :

　　　　$T_{\odot}(\mathbf{f}, \mathbf{g})=\frac{1}{\sqrt{d}}\left(\mathbf{R}_{\mathbf{f}} \mathbf{f}\right) \odot\left(\mathbf{R}_{\mathbf{g}} \mathbf{g}\right)$

　　其中 $\boldsymbol{R}_{\boldsymbol{f}}$, $\boldsymbol{R}_{g}$ 为训练过程中固定不变的随机矩阵，每个元素服从单方差对称分布, 适用分布包括均匀分布、高斯分布等; $\odot$ 表示矩阵对应位置元素相乘的操作; $d$ 表示抽取的维度数。

　　Note：显然公式是错误的 [ 矩阵左乘考虑的是样本之间的线性关系]，$\mathbf{R}_{\mathbf{f}} \mathbf{f}$ 和  $\mathbf{R}_{\mathbf{g}} \mathbf{g}$ 的维度都对不上，正确如下：

　　　　$T_{\odot}(\mathbf{f}, \mathbf{g})=\frac{1}{\sqrt{d}}\left( \mathbf{f} \mathbf{R}_{\mathbf{f}}\right) \odot\left( \mathbf{g}\mathbf{R}_{\mathbf{g}}\right)$

　　可证明 $T_{\odot}$  上进行内积近似 $T_{\otimes}$  上进行内积，且 $T_{\odot}$  是 $T_{\otimes}$  的无偏估计，以深度网络最大单无数 4096 作为阈值：

　　　　$T(\mathbf{h})=\left\{\begin{array}{ll}T_{\otimes}(\mathbf{f}, \mathbf{g}) & \text { if } d_{f} \times d_{g} \leqslant 4096 \\T_{\odot}(\mathbf{f}, \mathbf{g}) & \text { otherwise }\end{array}\right.$

2.4 熵调整(CDAN+E)

　　公式如下：

　　　　$\begin{array}{l}\underset{G}{\text{min}} \quad \mathbb{E}_{\left(\mathbf{x}_{i}^{s}, \mathbf{y}_{i}^{s}\right) \sim \mathcal{D}_{o}} L\left(G\left(\mathbf{x}_{i}^{s}\right), \mathbf{y}_{i}^{s}\right) \\ \quad\quad+\lambda\left(\mathbb{E}_{\mathbf{x}_{i}^{s} \sim \mathcal{D}_{s}} \log \left[D\left(T\left(\mathbf{h}_{i}^{s}\right)\right)\right]+\mathbb{E}_{\mathbf{x}_{j}^{t} \sim \mathcal{D}_{t}} \log \left[1-D\left(T\left(\mathbf{h}_{j}^{t}\right)\right)\right]\right) \\\end{array}$

　　　　$\underset{D}{\text{max}} \quad  \mathbb{E}_{\mathbf{x}_{i}^{s} \sim \mathcal{D}_{s}} \log \left[D\left(T\left(\mathbf{h}_{i}^{s}\right)\right)\right]+\mathbb{E}_{\mathbf{x}_{j}^{t} \sim \mathcal{D}_{t}} \log \left[1-D\left(T\left(\mathbf{h}_{j}^{t}\right)\right)\right]$

　　损失问题：条件域判别器的最大最小优化方法强制使不同的样本具有相同的重要性，可能导致不确定预测的难迁移样本也许会对抗适应产生不良影响

　　分类器预测不确定性的量化，使用熵定量预测的不确定性：

　　　　$H(\mathrm{~g})=-\sum_{c=1}^{C} g_{c} \log g_{c}$

　　预测的确定性则可表示为  $e^{-H(g)}$

　　损失改进：使用熵权重 $w(H(g))$调整条件域判别器接收的各个训练样本，使易于迁移的样本优先级更高，规避难迁移样本的影响：

　　　　$w(H(\mathbf{g}))=1+e^{-H(\mathbf{g})}$

　　熵调整后的损失函数：

　　　　$\begin{array}{l}\underset{G}{\text{min}} \quad \mathbb{E}_{\left(\mathbf{x}_{i}^{s}, \mathbf{y}_{i}^{s}\right) \sim \mathcal{D}_{s}} L\left(G\left(\mathbf{x}_{i}^{s}\right), \mathbf{y}_{i}^{s}\right) \\\quad+\lambda\left(\mathbb{E}_{\mathbf{x}_{i}^{s} \sim \mathcal{D}_{s}} w\left(H\left(\mathbf{g}_{i}^{s}\right)\right) \log \left[D\left(T\left(\mathbf{h}_{i}^{s}\right)\right)\right]+\mathbb{E}_{\mathbf{x}_{j}^{t} \sim \mathcal{D}_{t}} w\left(H\left(\mathbf{g}_{j}^{t}\right)\right) \log \left[1-D\left(T\left(\mathbf{h}_{j}^{t}\right)\right)\right]\right) \\\end{array}$

　　　　$\underset{D}{\text{max}} \quad  \mathbb{E}_{\mathbf{x}_{i}^{s} \sim \mathcal{D}_{s}} w\left(H\left(\mathbf{g}_{i}^{s}\right)\right) \log \left[D\left(T\left(\mathbf{h}_{i}^{s}\right)\right)\right]+\mathbb{E}_{\mathbf{x}_{j}^{t} \sim \mathcal{D}_{t}} w\left(H\left(\mathbf{g}_{j}^{t}\right)\right) \log \left[1-D\left(T\left(\mathbf{h}_{j}^{t}\right)\right)\right]$

　　Note：熵越大，权重越小；

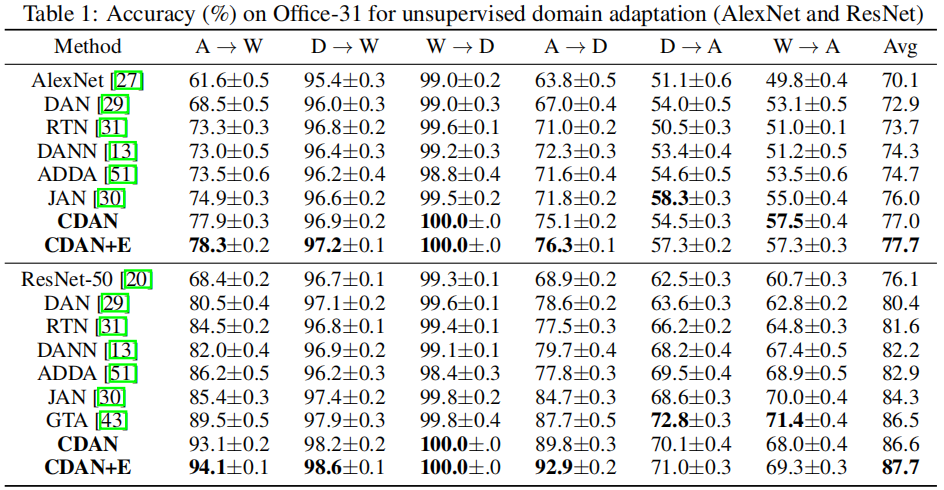
3 实验