hanoi（汉诺塔）递归实现

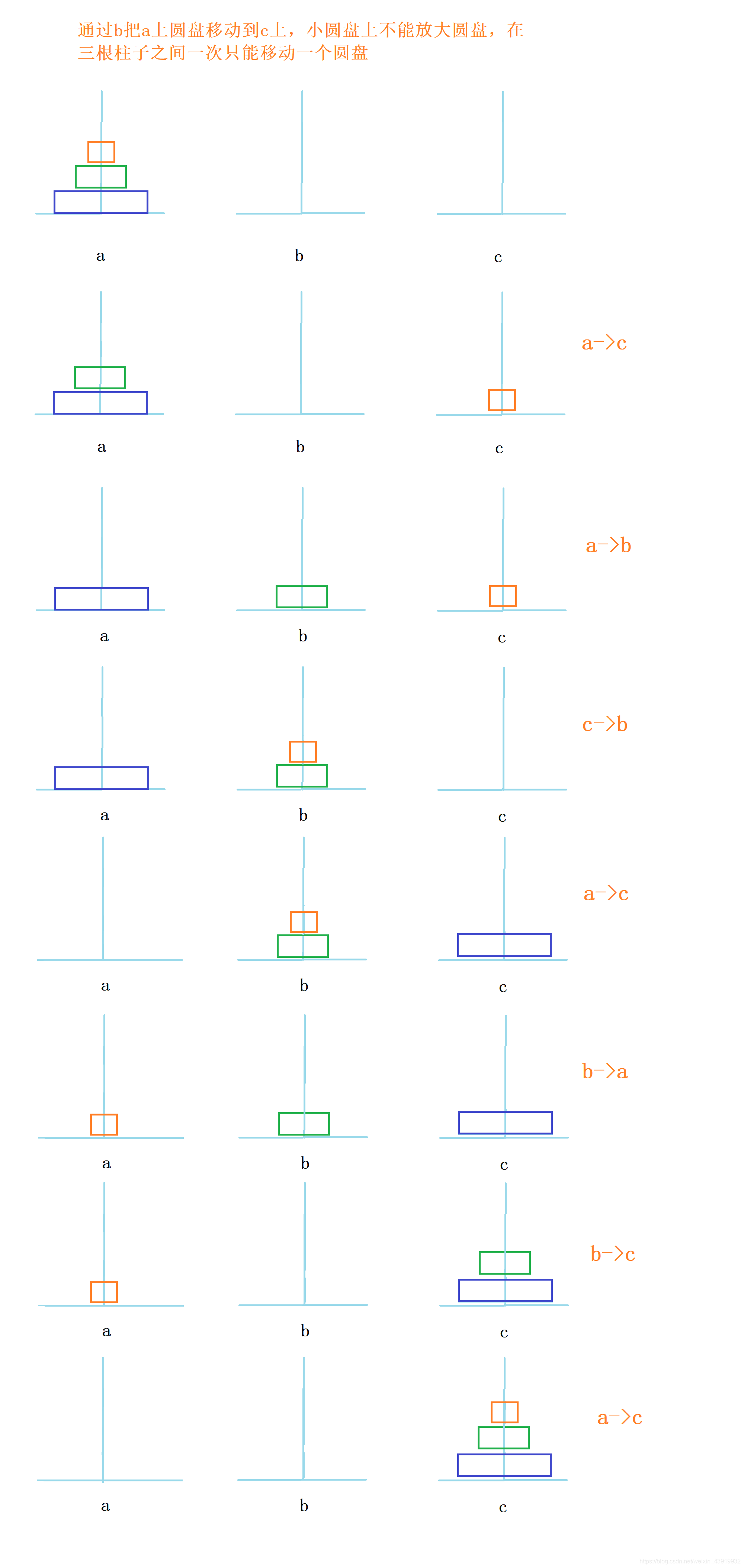
汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

三层汉诺塔的完整移动过程

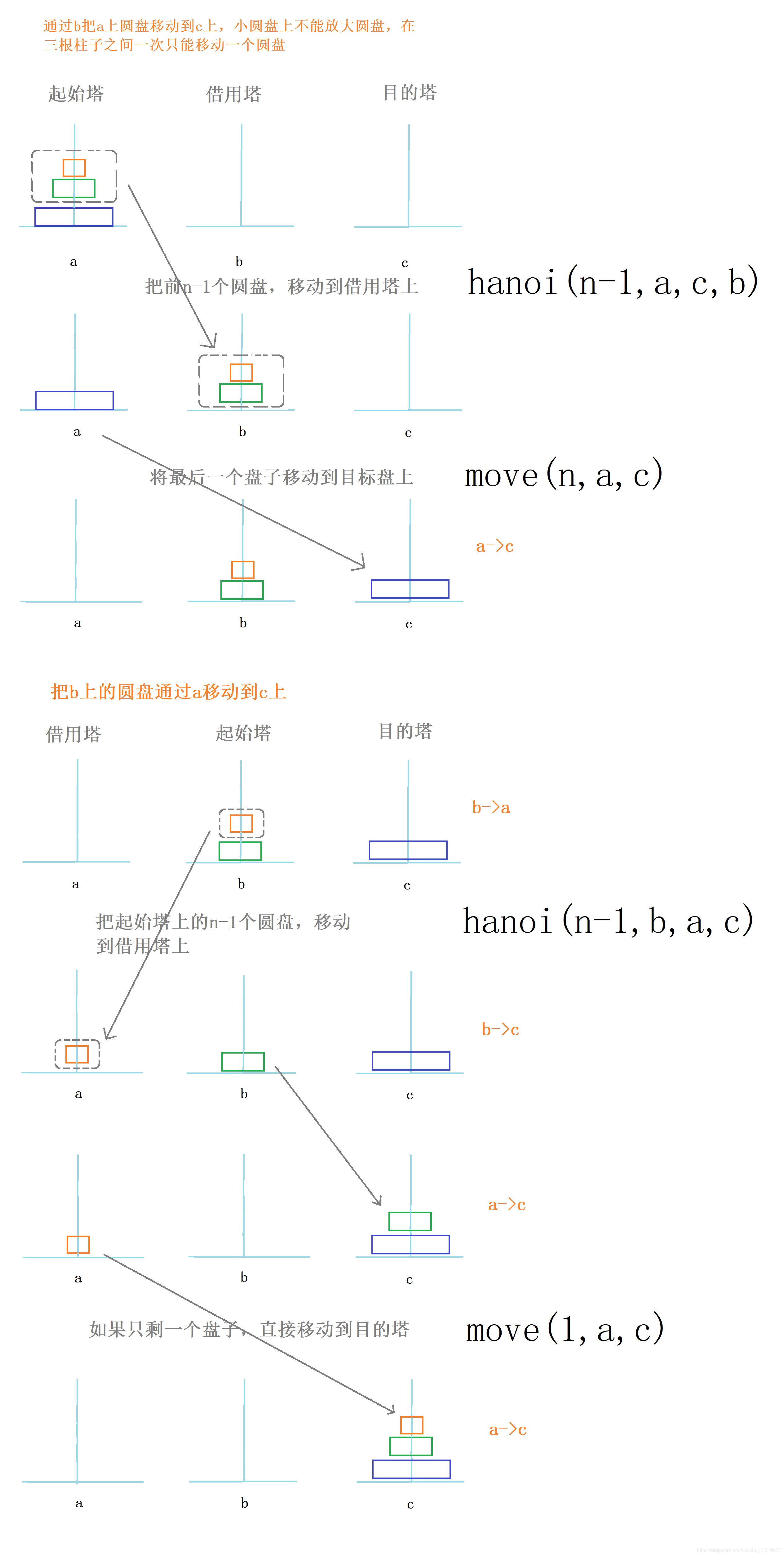
递归分析：利用递归的思想分析



通过以上图解的方式，发现三层汉诺塔最终可以转换成二层汉诺塔，同时只需要对一层的汉诺塔进行单独处理即可。同样的，四层汉诺塔、五层汉诺塔乃至n层汉诺塔最终都可以通过递归的方式转换成二层汉诺塔的求解，代码如下，仅供参考

#include<stdio.h>

void move(int n, char a, char c)
{
	printf("%c->%c\n", a, c);
}

void hanoi(int n, char a, char b, char c)//移动n个盘子，从a借助b到c
{
	if (n == 1)
		move(1, a, c);		//只剩一个盘子的时候
	else
	{
		hanoi(n-1, a, c, b);//将前n-1个盘子借助目的塔移动到借用塔上
		move(n, a, c);		//将剩下的一个盘子移动到目的塔上
		hanoi(n-1, b, a, c);//最后将借用塔上的n-1个盘子移动到目的塔上
	}
}

int main()
{
	hanoi(3,'a','b','c');	//测试三层汉诺塔
	return 0;
}

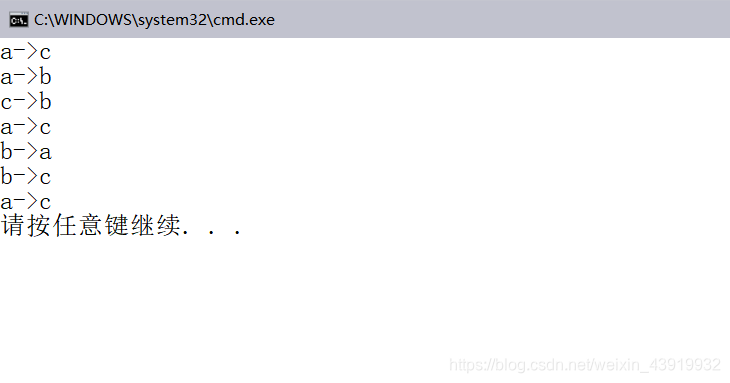
测试结果：