图-kruskal算法,prim算法
要求无向图
最小生成树: 连通性,累加和最小
并查集 结构
K算法
- 从最小的边开始,加上有没有形成环,没有就加,加上有环就不要
难点:如何判断加上一条边,有没有形成环。
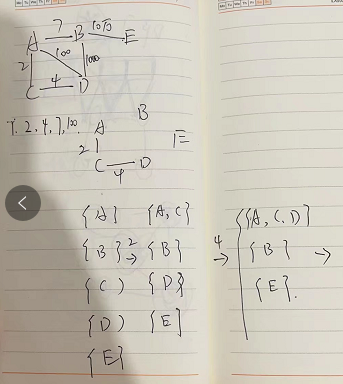
P算法
- 从点的角度开始
图-kruskal算法,prim算法的更多相关文章
- 最小生成树——Kruskal与Prim算法
最小生成树——Kruskal与Prim算法 序: 首先: 啥是最小生成树??? 咳咳... 如图: 在一个有n个点的无向连通图中,选取n-1条边使得这个图变成一棵树.这就叫“生成树”.(如下图) 每个 ...
- 图的最小生成树——Prim算法
Prim算法 Prim算法求最小生成树是采取蓝白点的思想,白点代表已经加入最小生成树的点,蓝点表示未加入最小生成树的点. 进行n次循环,每次循环把一个蓝点变为白点,该蓝点应该是与白点相连的最小边权的是 ...
- 图论篇2——最小生成树算法(kurskal算法&prim算法)
基本概念 树(Tree) 如果一个无向连通图中不存在回路,则这种图称为树. 生成树 (Spanning Tree) 无向连通图G的一个子图如果是一颗包含G的所有顶点的树,则该子图称为G的生成树. 生成 ...
- 最小生成树 kruskal算法&prim算法
(先更新到这,后面有时间再补,嘤嘤嘤) 今天给大家简单的讲一下最小生成树的问题吧!(ps:本人目前还比较菜,所以最小生成树最后的结果只能输出最小的权值,不能打印最小生成树的路径) 本Tianc在刚学的 ...
- 最小生成树(Kruskal和Prim算法)
关于图的几个概念定义: 关于图的几个概念定义: 连通图:在无向图中,若任意两个顶点vi与vj都有路径相通,则称该无向图为连通图. 强连通图:在有向图中,若任意两个顶点vi与vj都有路 ...
- 最小生成树的kruskal、prim算法
kruskal算法和prim算法 都说 kruskal是加边法,prim是加点法 这篇解释也不错:这篇 1.kruskal算法 因为是加边法,所以这个方法比较合适稀疏图.要码这个需要先懂并查集.因为我 ...
- 1.1.2最小生成树(Kruskal和Prim算法)
部分内容摘自 勿在浮沙筑高台 http://blog.csdn.net/luoshixian099/article/details/51908175 关于图的几个概念定义: 连通图:在无向图中,若任意 ...
- 算法导论--最小生成树(Kruskal和Prim算法)
转载出处:勿在浮沙筑高台http://blog.csdn.net/luoshixian099/article/details/51908175 关于图的几个概念定义: 连通图:在无向图中,若任意两个顶 ...
- Kruskal算法&Prim算法
最小生成树是什么? Kruskal算法 图文转载自a2392008643的博客 此算法可以称为"加边法",初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最 ...
- Kruskal和Prim算法求最小生成树
Kruskal算法求最小生成树 测试数据: 5 6 0 1 5 0 2 3 1 2 4 2 4 2 2 3 1 1 4 1 输出: 2 3 1 1 4 1 2 4 2 0 2 3 思路:在保证不产生回 ...
随机推荐
- 女朋友说:你要搞懂了MySQL三大日志,我就让你嘿嘿嘿!
1. 背景 MySQL实现事务.崩溃恢复.集群的主从复制,底层都离不开日志,所以日志是MySQL的精华所在.只有了解MySQL日志,才算是彻底搞懂MySQL. 今天一灯就带你深入浅出的学习MySQL的 ...
- S32Kxxx bootloader之UDS bootloader
了解更多关于bootloader 的C语言实现,请加我Q扣: 1273623966 (验证信息请填 bootloader),欢迎咨询或定制bootloader(在线升级程序). 两周前完成了基于UDS ...
- 网络通讯之Socket-Tcp(一)
网络通讯之Socket-Tcp 分成3部分讲解: 网络通讯之Socket-Tcp(一): 1.如何理解Socket 2.Socket通信重要函数 网络通讯之Socket-Tcp(二): 1.简单So ...
- 总结vue 需要掌握的知识点
使用的开发工具是webstorm,它是默认就安装好了vuejs插件,idea要使用的话,需要安装一下该插件 一.快速搭建项目vue-cli 脚手架(Vue2.0) 1.Vue CLI使用前提 –Nod ...
- day02 Java_变量
参考: 变量的练习: 声明一个变量,一次声明多个变量. 声明变量直接初始化,先声明变量,而后再给变量初始化. 声明整型变量g,声明另一个整型变量h并赋值为h+10,输出变量h的值. 声明整型变量i,在 ...
- Node.js精进(10)——性能监控(下)
本节会重点分析内存和进程奔溃,并且会给出相应的监控方法. 本系列所有的示例源码都已上传至Github,点击此处获取. 一.内存 虽然在 Node.js 中并不需要手动的对内存进行分配和销毁,但是在开发 ...
- 使用rust调用c++静态库并编译nodejs包
在项目上经常要用到身份证阅读器.护照阅读仪.指纹仪等各种品牌硬件,假如每套系统的都做集成开发那代码的维护成本将变得很高,为此采用rust来调用厂家提供的sdk c++开发包并封装成nodejs包,用f ...
- Odoo14 防暴力破解登录密码
1 # Odoo14 防暴力破解登录密码 2 # 主要工具:redis 3 # 实现思路:限制每个用户24小时内登录失败次数.连续超过5次失败后,需要等待一定时间后才能再次尝试登录 4 # 配置:在你 ...
- java反射的初理解
反射 获取类的方法: Class<?> aClass1 = Class.forName("TestDemo.refection.User");//通过类路径获取 Cla ...
- HttpServletRequest 类
目录 HttpServletRequest类有什么作用 HttpServletRequest 类的常用方法 如何获取请求参数 doGet 请求的中文乱码解决: POST 请求的中文乱码解决 请求的转发 ...
