SG函数&&SG定理

必胜点和必败点的概念：

       P点：必败点，换而言之，就是谁处于此位置，则在双方操作正确的情况下必败。

       N点：必胜点，处于此情况下，双方操作均正确的情况下必胜。

必胜点和必败点的性质：

        1、所有终结点是 必败点 P 。（我们以此为基本前提进行推理，换句话说，我们以此为假设）

        2、从任何必胜点N 操作，至少有一种方式可以进入必败点 P。

        3、无论如何操作，必败点P 都只能进入 必胜点 N。

下面通过例子介绍SG函数

定义mex(minimal excludant)运算，这是施加于一个集合的运算，表示最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。

对于任意状态 x ， 定义 SG(x) = mex(S),其中 S 是 x 后继状态的SG函数值的集合。如 x 有三个后继状态分别为 SG(a),SG(b),SG(c)，那么SG(x) = mex{SG(a),SG(b),SG(c)}。

对于SG函数有特殊的性质：

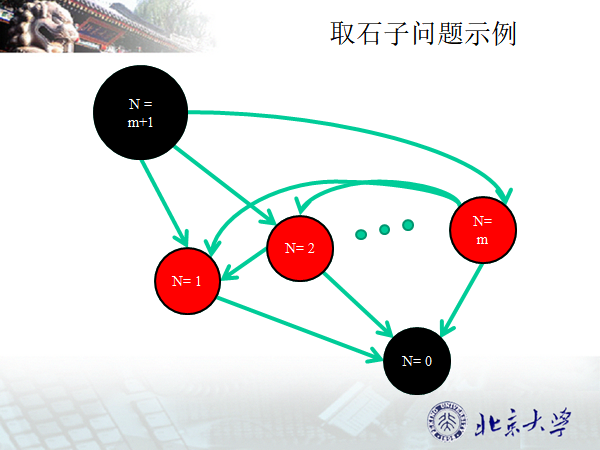
没有出边的点的SG值=0

对于可以到达SG=0的点的SG值>0

对于不能到达SG=0的点的SG值=0

和最开始的必胜态N和必败态P性质类似

必败态就是没有出边的点，SG = 0

可以到达必败态的点就是必胜态（SG>0）

不能到达必败态的点就是必败态（也就是说只能到达必胜态的点就是必败态，SG = 0）

多维度的情况

这里就是SG定理的运用：

游戏和的SG函数等于各个游戏SG函数的Nim和。这样就可以将每一个子游戏分而治之，从而简化了问题。而Bouton定理就是Sprague-Grundy定理在Nim游戏中的直接应用，因为单堆的Nim游戏 SG函数满足 SG(x) = x。