算法：LRU（最近最少使用）

算法：LRU（最近最少使用）

本文参考自小灰文章：https://mp.weixin.qq.com/s/B5xiVeW22ZumbI9KfrYJSg

LRU算法

什么是LRU算法

　　LRU算法又称最近最少使用算法，它的基本思想是长期不被使用的数据，在未来被用到的几率也不大，所以当新的数据进来时我们可以优先把这些数据替换掉。

　　在LRU算法中，使用了一种有趣的数据结构，称为哈希链表。我们知道哈希表是由多个<Key,Value>对组成的，哈希链表是将这写节点链接起来，每一个节点都有一个前驱结点和后驱节点，就像双向链表中的节点一样。哈希表拥有了固定的排列顺序。

　　

　　基于哈希链表的有序性，我们就可以把<Key,Value>按照最后的使用时间来排列。

LRU算法的基本思路

　　假设我们使用哈希链表来缓存用户信息，目前缓存了4个用户，用户按照时间顺序从链表右端插入：

　　

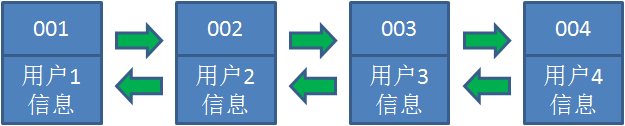
　　情景一：当访问用户5时，由于哈希链表中没有用户5的数据，从数据库中读取出来插入到缓存中

　　

　　情景二：挡访问用户2时，由于哈希链表中有用户2的数据，我们把它掐断，放到链表最右段

　　

　　

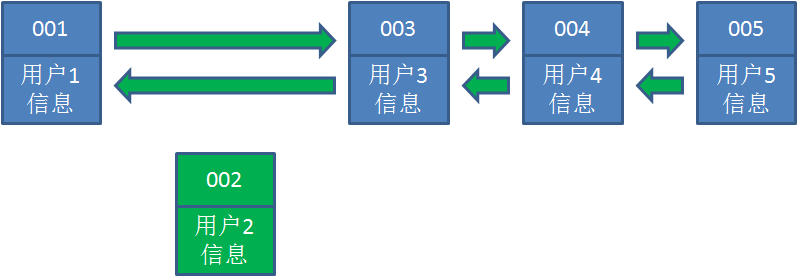
　　情景三：同情景二，这次访问用户4的数据

　　

　　情景四：当用户访问用户6，用户6在缓存中没有，需要插入到链表中，但此时链表长度已满，我们把最左端的用户删掉，然后插入用户6

　　

说明：我们仔细回顾一下，当缓存命中时，我们就把它放到最右端，也就是说排在右边的是最近被使用过的，那左边的当然是相对较少被访问过的，所以当缓存不命中的时候，我们就把最左边的剔除掉，所以这里就体现了最近最少使用的原则。

LRU算法的基本实现

public class LRUCache{
    private int limit;
    private HashMap<String,Node> hashMap;
    private Node head;
    private Node end;

    public LRUCache(int limit)
    {
        this.limit = limit;
        hashMap = new HashMap<String,Node>();
    }

    public String get(String key){
        Node node = hashMap.get(key);
        if(node ==null)
            return null;
        refreshNode(node);
        return node.value;
    }

    public void put(String key,String value){
        Node node = hashMap.get(key);
        if(node == null){
            if(hashMap.size()>=limit)
            {
                String oldKey = removeNode(head);
                hashMap.remove(oldKey);
            }
            node = new Node(key,value);
            addNode(node);
            hashMap.put(key,node)
        }else{
            node.value = value;
            refreshNode(node);
        }
    }

    public void remove(String key){
        Node node = hashMap.get(key);
        removeNode(node);
        hashMap.remove(key);
    }

    /**
     * 刷新刚被访问的节点位置
     */
    private void refreshNode(Node node)
    {
        if(node == end)
            return;
        removeNode(node);
        addNode(node);
    }

    /**
     * 删除节点
     */

    public String removeNode(Node node){
        if(node == end)
            //删除尾节点
            end = end.pre;
        else if(node ==head)
            //删除头节点
            head = head.next;
        else
            {
                //移除中间节点
                node.pre.next = node.next;
                node.next.pre = node.pre;
            }
        return node.key;
    }

    /**
     * 尾部插入节点
     */

     public void addNode(Node node)
     {
        if(end!=null)
        {
            end.next = node;
            node.pre = end;
            node.next = null;
        }
        end = node;
        if(head == null)
            head = node;
     }

}