C++-POJ3233-Matrix Power Series[矩阵乘法][快速幂]

构造矩阵

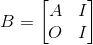
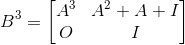
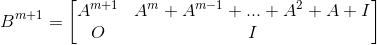
 #include <cstdio>
 const int MAXN=;
 struct Matrix{int a[MAXN][MAXN];}O,I;int N;
 void OI(int n){N=n;for(int i=;i<MAXN;i++)for(int j=;j<MAXN;j++)O.a[i][j]=,I.a[i][j]=(i==j);}
 Matrix Mul(Matrix A,Matrix B,int MOD){
     Matrix C=O;
         for(int i=;i<=N;i++)
             for(int j=;j<=N;j++)
                 for(int k=;k<=N;k++)
                     C.a[i][j]=(C.a[i][j]+A.a[i][k]*B.a[k][j])%MOD;
     return C;
 }
 Matrix Pow(Matrix A,int n,int MOD){
     Matrix B=I;
     for(;n;A=Mul(A,A,MOD),n>>=)if(n&)B=Mul(B,A,MOD);
     return B;
 }
 Matrix B(int n){
     Matrix B=O;
     for(int i=;i<=n;i++)
         for(int j=;j<=n;j++)
             scanf("%d",&B.a[i][j]);
     for(int i=;i<=n;i++)
         B.a[i+n][i+n]=B.a[i][i+n]=;
     return B;
 }
 int main(){
     int n,m,k;scanf("%d%d%d",&n,&m,&k),OI(*n);
     Matrix A=Pow(B(n),m+,k);
     for(int i=;i<=n;i++){
         for(int j=;j<=n;j++)
             printf("%d ",(A.a[i][j+n]-(i==j)+k)%k);
         puts("");
     }
     return ;
 }