ACM-ICPC 2018 沈阳赛区网络预赛-B，F，G

学长写的

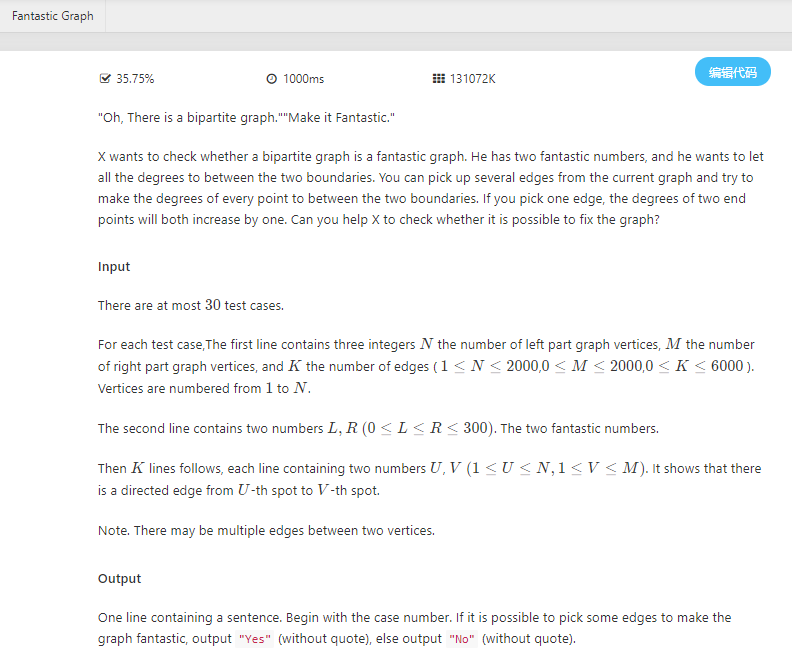
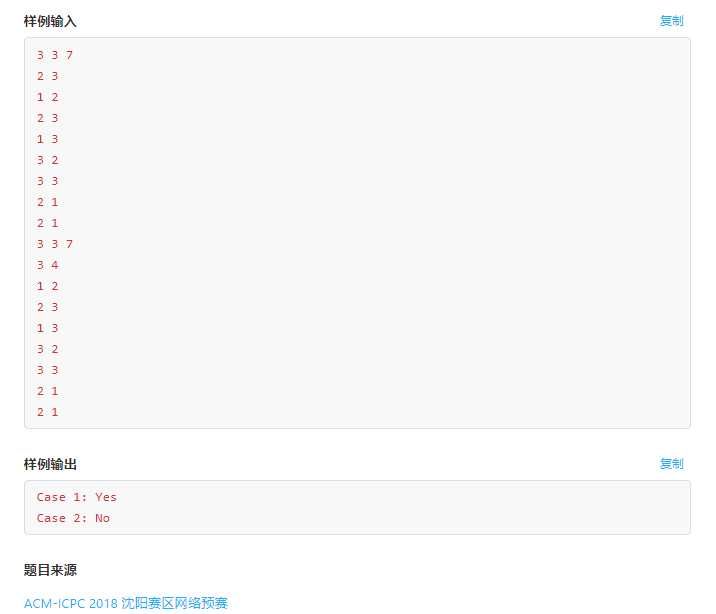
F. Fantastic Graph

"Oh, There is a bipartite graph.""Make it Fantastic."

X wants to check whether a bipartite graph is a fantastic graph. He has two fantastic numbers, and he wants to let all the degrees to between the two boundaries. You can pick up several edges from the current graph and try to make the degrees of every point to between the two boundaries. If you pick one edge, the degrees of two end points will both increase by one. Can you help X to check whether it is possible to fix the graph?

Input

There are at most 3030 test cases.

For each test case,The first line contains three integers NN the number of left part graph vertices, MM the number of right part graph vertices, and KK the number of edges ( 1 \le N \le 20001≤N≤2000,0 \le M \le 20000≤M≤2000,0 \le K \le 60000≤K≤6000 ). Vertices are numbered from 11 to NN.

The second line contains two numbers L, RL,R (0 \le L \le R \le 300)(0≤L≤R≤300). The two fantastic numbers.

Then KK lines follows, each line containing two numbers UU, VV (1 \le U \le N,1 \le V \le M)(1≤U≤N,1≤V≤M). It shows that there is a directed edge from UU-th spot to VV-th spot.

Note. There may be multiple edges between two vertices.

Output

One line containing a sentence. Begin with the case number. If it is possible to pick some edges to make the graph fantastic, output "Yes" (without quote), else output "No" (without quote).

#include<bits/stdc++.h>
#define LL long long
#define INF 0x3f3f3f3f
#define inf 0x3f3f3f3f
#define fi first
#define se second
using namespace std;
const int maxn = 6e3+32;
int n,m,k;
int du[2000+42];
int du2[2000+32];
int L,R;
const int MX = 4000+54;
const int MXE = 19000+43;
struct MaxFlow
{
    struct Edge
    {
        int v, w, nxt;
    } edge[MXE],edge2[MXE];
    int tot, num, s, t;
    int head[MX];
    void init()
    {
        memset(head, -1, sizeof(head));
        tot = 0;
    }
    void add(int u, int v, int w)
    {
        edge[tot].v = v;
        edge[tot].w = w;
        edge[tot].nxt = head[u];
        head[u] = tot++;

        edge[tot].v = u;
        edge[tot].w = 0;
        edge[tot].nxt = head[v];
        head[v] = tot++;
    }

    int  d[MX], vis[MX], gap[MX];
    void bfs()
    {
        memset(d, 0, sizeof(d));
        memset(gap, 0, sizeof(gap));
        memset(vis, 0, sizeof(vis));
        queue<int>q;
        q.push(t);
        vis[t] = 1;
        while (!q.empty())
        {
            int u = q.front();
            q.pop();
            for (int i = head[u]; ~i; i = edge[i].nxt)
            {
                int v = edge[i].v;
                if (!vis[v])
                {
                    d[v] = d[u] + 1;
                    gap[d[v]]++;
                    q.push(v);
                    vis[v] = 1;
                }
            }
        }
    }

    int last[MX];
    int dfs(int u, int f)
    {
        if (u == t) return f;
        int sap = 0;
        for (int i = last[u]; ~i; i = edge[i].nxt)
        {
            int v = edge[i].v;
            if (edge[i].w > 0 && d[u] == d[v] + 1)
            {
                last[u] = i;
                int tmp = dfs(v, min(f - sap, edge[i].w));
                edge[i].w -= tmp;
                edge[i ^ 1].w += tmp;
                sap += tmp;
                if (sap == f) return sap;
            }
        }
        if (d[s] >= num) return sap;
        if (!(--gap[d[u]])) d[s] = num;
        ++gap[++d[u]];
        last[u] = head[u];
        return sap;
    }

    int solve(int st, int ed, int n)
    {
        int flow = 0;
        num = n;
        s = st;
        t = ed;
        bfs();
        memcpy(last, head, sizeof(head));
        while (d[s] < num) flow += dfs(s, inf);
        return flow;
    }
} F;
int S,T;
void update(int u,int v,int L,int R)
{
    F.add(u,v,R-L);
    F.add(S, v, L);
    F.add(u, T, L);

}
pair<int,int>Q[6000+53];

int main()
{
    int ka = 1;
    while(~scanf("%d%d%d",&n,&m,&k))
    {
        F.init();
        S = n+m+2;
        T = n+m+3;
        F.add(n+m+1, 0, INF);
        for(int i = 0;i<=max(n,m);i++){
            du[i] = du2[i] = 0;
        }
        scanf("%d%d",&L,&R);

        for(int i = 1;i<=n;i++){
            update(0,i,L,R);
        }
        for(int i = n+1;i<=n+m;i++)
        {
            update(i,n+m+1,L,R);
        }

        for(int i = 0;i<k;i++){
            int u,v;
            scanf("%d%d",&u,&v);
            Q[i].first = u;
            Q[i].second = v;
            du[u]++;
            du2[v]++;
            F.add(u, v+n, 1);
        }
    printf("Case %d: ",ka++);
        int ret = F.solve(S, T, T + 11);
        if(ret != (n+m)*L) puts("No");
        else puts("Yes");
    }
}

B. Call of Accepted

You and your friends are at the table, playing an old and interesting game - the Call of Cthulhu.

There is a mechanism in the game: rolling the dice. You use a notation to communicate the type of dice that needs to be rolled - the operator "\mathop{\rm d}d". "x\mathop{\rm d}yxdy" means that an yy-sided dice should be rolled xx times and the sum of the results is taken.

Formally, for any two integers x, yx,y satisfying x \geq 0x≥0 and y \geq 1y≥1 , "x\mathop{\rm d}yxdy" means the sum of xx random integers in the range of [1, y][1,y]. It's obvious that either x < 0x<0 or y < 1y<1 makes the expression x\ {\rm d}\ yx d y illegal. For example: "2\mathop{\rm d}62d6" means that rolling a 66-sided dice 22 times. At this time, the result can be at least [1, 1] = 2[1,1]=2, and at most [6, 6] = 12[6,6]=12. The results of rolling can be used extensively in many aspects of the game. For example, an "1\mathop{\rm d}1001d100" can be used to determine whether an action with a percentage probability is successful, and a "3\mathop{\rm d}6+33d6+3 * 22" can be used to calculate the total damage when being attacked by 33 monsters simultaneously. In particular, the precedence of "\mathop{\rm d}d" is above "*". Since the operator "\mathop{\rm d}d" does not satisfy the associative law, it's necessary to make sure that "\mathop{\rm d}d" is right-associative.

Now the game has reached its most exciting stage. You are facing the Great Old One - Cthulhu. Because the spirit has been greatly affected, your sanity value needs to be deducted according to the result of rolling. If the sanity value loses too much, you will fall into madness. As a player, you want to write a program for knowing the minimum and maximum loss of sanity value before rolling, in order to make a psychological preparation.

The oldest and strongest emotion of mankind is fear, and the oldest and strongest kind of fear is fear of the unknown. ----H. P. Lovecraft

Input

There are multiple sets of input, at most 3030 cases.

Each set of input contains a string of only '+', '-', '*', 'd', '(', ')' and integers without spaces, indicating the expression of this sanity loss. The length of the expression will be at most 100100.

It is guaranteed that all expressions are legal, all operators except for '(' and ')' are binary, and all intermediate results while calculating are integers in the range of [-2147483648, 2147483647][−2147483648,2147483647].

The most merciful thing in the world, I think, is the inability of the human mind to correlate all its contents. We live on a placid island of ignorance in the midst of black seas of infinity, and it was not meant that we should voyage far. ----H. P. Lovecraft

Output

For each set of data, output a line of two integers separated by spaces, indicating the minimum and maximum possible values of the sanity loss.

#include<bits/stdc++.h>
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define x first
#define y second
#define rep(i,a,b) for(int i=a;i<(b);++i)
#define per(i,a,b) for(int i=a-1;i>=(b);--i)
#define fuck(x) cout<<'['<<#x<<' '<<(x)<<']'
#define sub(x,y) x=((x)-(y)<0)?(x)-(y)+mod:(x)-(y)
#define clr(a,b) memset(a,b,sizeof(a))
#define eps 1e-10
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int> VI;
typedef pair<int, int> PII;
typedef unsigned int ui;
const int INF = 0x3f3f3f3f;
const ll INFLL = 0x3f3f3f3f3f3f3f3fLL;
const int mod = 1e9 + 7;
const int MX = 2e6 + 5;

vector<string>pre, s;
string str;

bool isoperator(string op) {
    if(op == "+" || op == "-" || op == "*" || op == "d") return 1;
    return 0;
}
int priority(string op) {
    if(op == "#") return -1;
    if(op == "(") return 0;
    if(op == "+" || op == "-") return 1;
    if(op == "*") return 2;
    if(op == "d") return 3;
    return -1;
}

void postfix() {
    stack<string> OPTR;   //运算符栈
    stack<string> OPND;   //数据栈

    OPTR.push("#");
    rep(i, 0, pre.size()) {
        if (pre[i] == "(") OPTR.push(pre[i]);
        else if(pre[i] == ")") {
            while(OPTR.top() != "(") {
                OPND.push(OPTR.top());
                OPTR.pop();
            }
            OPTR.pop();
        } else if (isoperator(pre[i])) {
            while(!OPTR.empty() && (priority(pre[i]) < priority(OPTR.top()) || priority(pre[i]) == priority(OPTR.top()) && pre[i] != "d")) {
                OPND.push(OPTR.top());
                OPTR.pop();
            }
            OPTR.push(pre[i]);
        } else OPND.push(pre[i]);
    }

    while(OPTR.top() != "#") {
        OPND.push(OPTR.top());
        OPTR.pop();
    }
    OPTR.pop();

    //利用操作符栈逆序即可得到后缀表达式
    while(!OPND.empty()) {
        OPTR.push(OPND.top());
        OPND.pop();
    }

    s.clear();
    while(!OPTR.empty()) {
        s.push_back(OPTR.top());
        OPTR.pop();
    }
}

bool is_dig(char ch) {return ch >= '0' && ch <= '9';}
void pre_solve() {
    pre.clear();
    rep(i, 0, str.length()) {
        if(is_dig(str[i])) {
            rep(j, i, str.length()) {
                if(!is_dig(str[j])) {
                    pre.push_back(str.substr(i, j - i));
                    i = j - 1;
                    break;
                }
                if(j == str.length() - 1) {
                    pre.push_back(str.substr(i, j - i + 1));
                    i = j;
                    break;
                }
            }
        } else pre.push_back(str.substr(i, 1));
    }
}
ll str_to_int(string st) {
    ll ret = 0;
    rep(i, 0, st.length()) ret = ret * 10 + st[i] - '0';
    return ret;
}

struct node {
    ll l, r;
    node(ll l = 0, ll r = 0): l(l), r(r) {}
    node(string st) {l = r = str_to_int(st);}
    node operator-(const node& _A)const {
        return node(l - _A.r, r - _A.l);
    }
    node operator+(const node& _A)const {
        return node(l + _A.l, r + _A.r);
    }
    node operator*(const node& _A)const {
        node ret;
        ll a = l * _A.l;
        ll b = l * _A.r;
        ll c = r * _A.l;
        ll d = r * _A.r;
        ret.l = min(min(a, b), min(c, d));
        ret.r = max(max(a, b), max(c, d));
        return ret;
    }
    node operator/(const node& _A)const {
        node ret;
        ll l1 = max(l, 0ll), r1 = r;
        ret.l = l1, ret.r = r1 * _A.r;
        return ret;
    }
};

int main() {
#ifdef local
    freopen("in.txt", "r", stdin);
#endif // local
    while(cin >> str) {
        pre_solve();
        postfix();
        stack<node>stk;
        node a, b;
        rep(i, 0, s.size()) if(isoperator(s[i])) {
            b = stk.top(); stk.pop();
            a = stk.top(); stk.pop();
//            printf("[%lld %lld]\n", a.l, a.r);
//            printf("[%lld %lld]\n", b.l, b.r);
            if(s[i] == "-") a = a - b;
            if(s[i] == "+") a = a + b;
            if(s[i] == "*") a = a * b;
            if(s[i] == "d") a = a / b;
            stk.push(a);
        } else stk.push(node(s[i]));
        a = stk.top();
        printf("%lld %lld\n", a.l, a.r);
    }
    return 0;
}

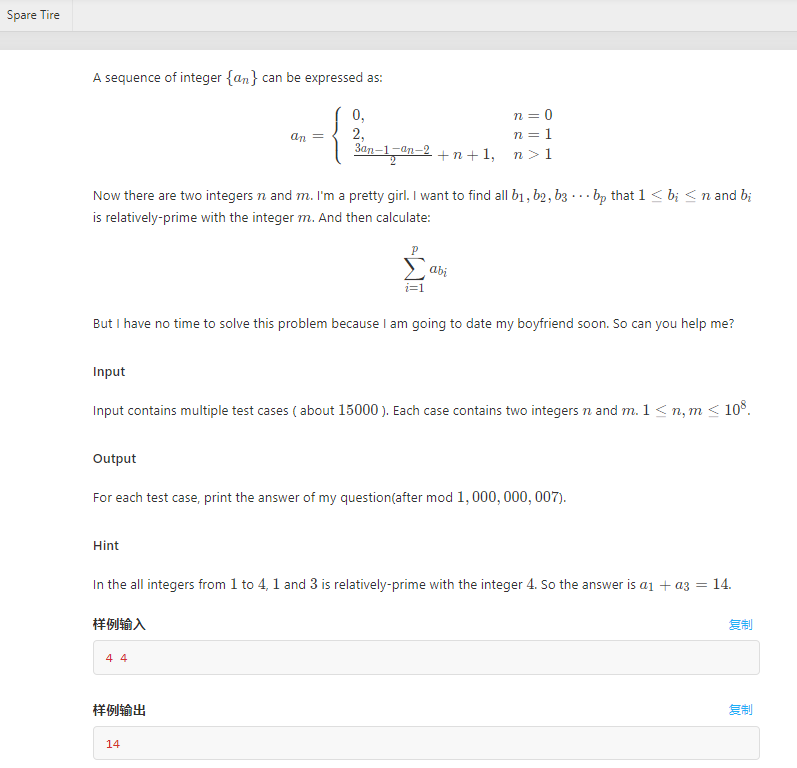
G.Spare time



\(a_{n} = a_{n-1}+2\times n\)

\(a_{n} = (a_{n}-a_{n-1})+(a_{n-1}-a_{n-2})+...+(a_{2}-a_{1})+a_{1} = n\times (n+1)\)

\(S_{n} = \sum_{i=1}^n i\times(i+1) = n\times(n+1)/2 + n\times(n+1)\times(2n+1)/6\)

 利用容斥思想，如当\(m=6\)时，有\(2\)，\(3\)两个质因子。既然要求与\(m\)互素的下标的数之和，我们枚举素因子的倍数，二进制枚举最简的倍数。

 当枚举到\(2\)时，要删去\(2(2*1)，4(2*2)，6(2*3)\)；当枚举到\(3\)时，要删去\(3(3*1)，6(3*2)\)；(注意到\(6\)被删了两次)；当枚举到\(6\)时，要加上\(6\)哦。

容斥：

令\(tmp = tot*get\_num1(cnt)+tot*tot*get\_num2(cnt);\)

tmp = tot*get_num1(cnt)+tot*tot*get_num2(cnt);

若tot是偶数个质因子的倍数，答案加上这个数及其倍数的贡献，即tmp。

若tot是奇数个质因子的倍数，答案减去这个数及其倍数的贡献，即tmp。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD = (LL)1e9 + 7;
LL n, m, inv2, inv6;
vector<int> ve;
LL inv(LL t){
  return t == 1LL? 1LL: (MOD-MOD/t)*inv(MOD%t)%MOD;
}
LL get_num1(LL n){
  return n*(n+1)%MOD*inv2%MOD;
}
LL get_num2(LL n){
  return n*(n+1)%MOD*(2*n%MOD+1)%MOD*inv6%MOD;
}
int main(){
  inv2 = inv(2), inv6 = inv(6);
  while(~scanf("%lld%lld", &n, &m)){
    ve.clear();
    int tm = m;
    for(int i = 2; (LL)i * i <= m && i <= n; ++i){
      if(tm % i == 0){
        ve.push_back(i);
        while(tm % i == 0)tm /= i;
      }
      if(tm == 1)break;
    }
    if(tm != 1)ve.push_back(tm);
    int len = ve.size(), state = 1 << len;
    LL ans = (get_num1(n)+get_num2(n))%MOD;
    ans = 0;
    for(int i = 0; i < state; ++i){
      LL tot = 1, cnt;
      int num = 0;
      for(int j = 0; j < len; ++j){
        if(i&(1<<j)){
          ++num;
          tot *= ve[j];
        }
      }
      cnt = n/tot;
      //printf("*%lld %lld %d\n", tot,cnt,num);
      if(num % 2 == 0){
        ans = (ans+ tot*tot%MOD*get_num2(cnt)%MOD+tot*get_num1(cnt)%MOD)%MOD;
      }else{
        ans = (ans- tot*tot%MOD*get_num2(cnt)%MOD-tot*get_num1(cnt)%MOD)%MOD;
        ans = (ans + MOD)%MOD;
      }
    }
    printf("%lld\n", ans);
  }
  return 0;
}

#### HDU6397容斥

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>

using namespace std;

typedef long long LL;

const int MXN = 3e5 + 6;
const int MXT = 1e5 + 5;
const int mod = 998244353;

LL n, m, k;
LL f[MXN], invF[MXN];
LL niyuan(int t) {
    return t == 1? 1: (mod-mod/t)*niyuan(mod%t)%mod;
}
LL ksm(LL a, int b) {
    LL ans = 1;
    while(b) {
        if(b&1) ans = ans * a %mod;
        b >>= 1;
        a = a * a %mod;
    }
    return ans;
}
void init() {
    f[0] = 1; invF[0] = 1;
    for(int i = 1; i < MXN; ++i) f[i] = f[i-1] * i % mod;
    //invF[MXN-1] = niyuan(f[MXN-1]);
    invF[MXN-1] = ksm(f[MXN-1], mod-2);
    for(int i = MXN-2; i >= 1; --i) invF[i] = invF[i+1]*(i+1)%mod;
}
LL COMB(LL n, LL m) {
    if(n < m) return 0;
    return f[n] * invF[m] % mod * invF[n-m] % mod;
}
int main(int argc, char const *argv[]) {
#ifndef ONLINE_JUDGE
    //freopen("E://ADpan//in.in", "r", stdin);
#endif
    init();
    int tim;
    scanf("%d", &tim);
    while(tim--) {
        scanf("%lld%lld%lld", &n, &m, &k);
        LL ans = COMB(k+m-1,m-1), tmp;
        for(int i = 1; i <= m; ++i) {
            tmp = COMB(k+m-i*n-1, m-1) * COMB(m, i) % mod;
            if(i & 1) ans = (ans - tmp + mod)%mod;
            else ans = (ans + tmp)%mod;
        }
        printf("%lld\n", ans);
    }
    return 0;
}

/*
字母xi=[0,n-1],问有多少个长度为m的单词,其和为k
*/