JAVA数据结构之二叉树

　　用树作为存储数据的结构兼具像数组一样查询速度快和像链表一样具有很快的插入和删除数据项的优点

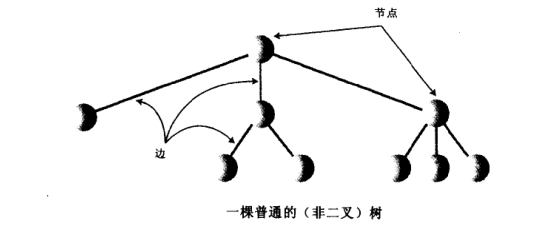
　　我们用圆点表示节点，连接圆的直线表示边如下图所示就表示了一颗树，接下来我们讨论的二叉树即每个节点最多只有两个子节点的树称作是二叉树。除了二叉树还有多路树，比如2-3-4树和外部存储就属于多路树

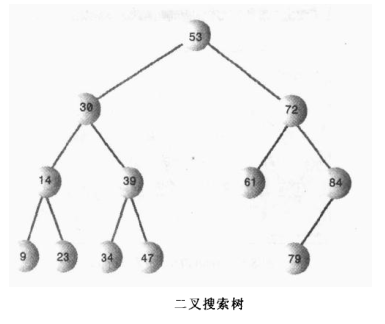
　　二叉搜索树：一个节点的左子节点关键字小于这个节点，右子节点关键字大于或等于这个父节点，

　　在java中我们要设计一个树可以只用下面的代码

class Node{　　　//树节点类　　　　　　　　　class Person{ //封装树节点的数据　　class Tree{ //相当于树的根节点

　　Person person;　　　　　　　　　　　　　　int iData;　　　　　　　　　　　　　　private Node root;

　　Node leftChild;　　　　　　　　　　　　　　double dData;　　　　　　　　　　　　 //包含一些操作树的方法

　　Node rightChild;　　　　　　　　　　　　 }　　　　　　　　　　　　　　　　}

}　　　　　　　　　　　　　　　　　

二叉树查找元素

　　下图展示了在搜索二叉树中查找关键值为57的节点的查找流程图

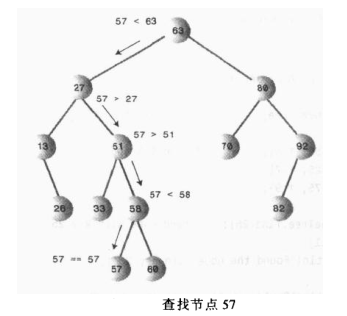
由上图我们可以写出上面的们Tree类中的查找的方法

public Node find ( int key ){
　　Node current = root;
　　while(current.iData != key){
　　　　if(key < current.iData){
　　　　　　current = current.leftChild;
　　　　}else{
　　　　　　current = current.rightChild;
　　　　}
　　　　if(current == null){ //说明此时没有找到对应的节点
　　　　　　return null;
　　　　}　　
　　}
　　return current; //循环执行结束跳出循环，说明找到此关键字节点，返回节点
}

　　这里我们可以总结出在树中查找节点的效率，首先取决于关键字所在树的层数，像我们图中给出的树最多5层，即查找最多进行5次比较，节点数最多为31准确来说所需要的时间复杂度为O(log₂N)

二叉树插入节点

　　接下来讨论在树中插入一个节点：插入的方法和查找很像，只不过插入在最后一步遇到null不是立即返回null，而需要在返回之前插入节点

public void insert( int id,double dd){
　　Node newNode = new Node; //创建新的节点
　　newNode.iData = id;
　　newNode.dData = dd;
　　if(root == null){
　　　　root = newNode;
　　}else{
　　　　Node current = root;
　　　　Node parent; //引入parent是为了记录新节点插入的位置，不然当找到插入的地方会去其插入的父节点的位置
　　　　while(true){
　　　　　　parent = current;
　　　　　　if(id< current.iData){
　　　　　　　　current = current.leftChild;
　　　　　　　　if(current == null){ //说明此时没有找到对应的节点,将新节点连入左子节点
　　　　　　　　　　parrent.leftChild = newNode;
　　　　　　　　　　return;
　　　　　　　　}　
　　　　　　}else{
　　　　　　　　current = current.rightChild;
　　　　　　　　if(current == null){ //说明此时没有找到对应的节点,将新节点连入右子节点
　　　　　　　　　　parrent.rightChild= newNode;
　　　　　　　　　　return;
　　　　　　　　}　
　　　　　　}
　　　　}
　　}
}

遍历二叉树　　

　　接下来我们介绍遍历一个二叉树：我们常用的遍历树的方法有三种：前序，中序，后序。二叉树中常用的遍历方式是中序遍历，这里我们遍历的方法只需要做三件事情，1.调用自身来遍历节点的左子树，2.访问这个节点，3.调用自身来遍历节点的右子树，下面是java代码

public void inOrder(Node localRoot){ 　　 //使用递归的方式来遍历一颗树
　　if(localRoot != null){
　　　　inOrder(localRoot.leftChild);　　　　 //遍历左子树
　　　　System.out.print(localRoot.iData+" ");　　 //访问自身数据
　　　　inOrder(localRoot.rightChild);　　 //遍历右子树
　　}
}

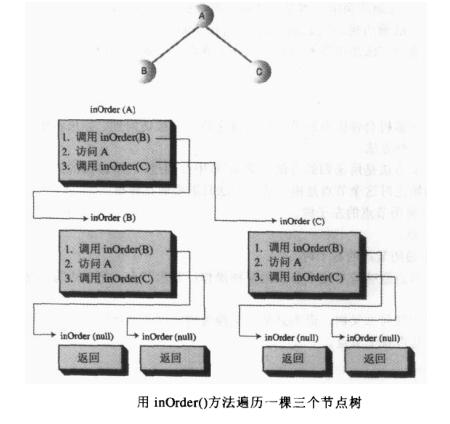
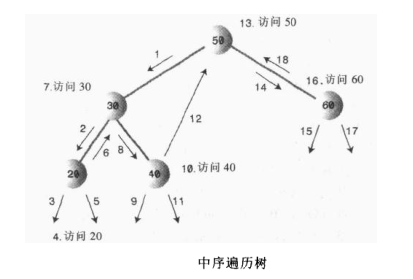
　　前序遍历步骤：1.访问这个节点，2.调用自身来遍历节点的左子树，3.调用自身来遍历节点的右子树

　　后序遍历步骤：1.调用自身来遍历节点的左子树，2.调用自身来遍历节点的右子树，3.访问这个节点

　　查找二叉搜索树中的最大最小值：最小值一直往树的最左边往下查找即可得到最小值，相反向右可得到最大值。

public Node minimum(){ 　　 //查找二叉搜索树中的最小值
　　Node current，last;
　　current = root;
　　while(current != null){
last = current;
current = current.leftChild; //将这里换成Right即可查询的到最大值
}
return last;
}

删除二叉树中的节点　　

　　接下来介绍二叉树如何删除一个节点，要删除二叉树的节点我们需要考虑到三种删除的状态：

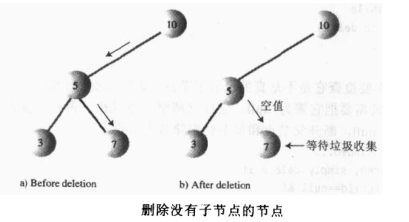
　　　　1.该节点是叶节点，是叶节点的情况删除很简单，只需要将父节点对应的子节点改为null即可，如图

　　　　2.节点有一个子节点，删除该节点，只需要将需要删除的节点的唯一一个子节点连接到需要删除的节点的父节点之上，如图

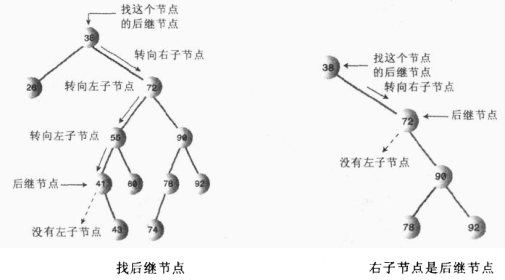
　　　　3.有两个子节点，若有两个子节点，则需要找到该删除节点的中序后继节点来替换当前删除的节点（找后继节点的算法简单来说就是先向该节点右边找到子节点，然后一直往左边找到最小值即可得到该节点的后继节点）

接下来写出完整的删除节点的java代码

public boolean delete(int key){
　　Node current = root;
　　Node parent = root;
　　boolean isLeftChild = true;
　　while(current.iData != key){
　　　　parent = current;
　　　　if(key < current.iData){
　　　　　　isLeftChild = true;
　　　　　　current = current.leftChild;
　　　　}else{
　　　　　　isLeftChild = false;
　　　　　　current = current.rightChild;
　　　　}
　　　　if(current == null){
　　　　　　return;　　　　//没有找到需要删除的数据项，直接返回
　　　　}
　　}
　　//1.如果删除的节点是叶子结点，直接删除
　　if(current.leftChild == null && current.rightChild == null){
　　　　if(current == root){
　　　　　　root = null;
　　　　}else if(isLeftChild){
　　　　　　parent.leftChild = null;
　　　　}else{
　　　　　　parent.rightChild = null;
　　　　}
　　}else if(current.rightChild == null){ //删除的节点只有左子节点
　　　　if(current == root){
　　　　　　root = current.leftChild;
　　　　}else if(isLeftChild){
　　　　　　parent.leftChild = current.leftChild;
　　　　}else{
　　　　　　parent.rightChild = current.leftChild ;
　　　　}
　　}else if(current.leftChild == null){ //删除的节点只有右子节点
　　　　if(current == root){
　　　　　　root = current.leftChild;
　　　　}else if(isLeftChild){
　　　　　　parent.leftChild = current.rightChild ;
　　　　}else{
　　　　　　parent.rightChild = current.rightChild ;
　　　　}
　　}else{
　　　　Node successor = getSuccessor(current); //查找得到删除节点的后继
　　　　if(current == root){
　　　　　　root = successor;
　　　　}else if(isLeftChild){
　　　　　　parent.leftChild = successor;
　　　　}else{
　　　　　　parent.rightChild = successor;
　　　　}
　　 successor.leftChild = current.leftChild; //最后一步设置删除替换后的左子节点
　　}
}
//查找后继节点的算法
private Node getSuccessor(Node delNode){
　　Node successorParent = delNode;
　　Node successor = delNode;
　　Node current = delNode.rightChild;
　　While(current!=null){
　　　　successorParent = successor;
　　　　successor = current;
　　　　current = current.leftChild;
　　}
　　if(successor != delNode.rightChild){
　　　　successorParent.leftChild = successor.rightChild;//将后继节点的父节点的左子节点值设置为后继的右子节点
　　 successor.rightChild = delNode.rightChild;//将后继节点的右子节点设置成当前删除节点的右子节点（处理后）
　　}
　　return successor;
}

二叉树的效率

二叉树的效率：二叉树的效率取决于二叉树的层数(层数即为操作时最多的比较次数)，下表给出了一个二叉满树的节点数和层数的关系，我们可以设第一列节点数为N层数为L，那么

N = 2^L-1 <=> L = (log₂N+1)

这里我们能换算成大O表示的时间复杂度为O(logN)。同样层数的不满的树的用时是要小于满树的时间的，树对于常用的数据存储操作有很高的效率，遍历不如其他的操作快。