FFT初步代码分析和逼近曲线

FFT：快速傅里叶变换

　　文章从两个方面来写，一个是FFT的基础知识，也就是将时域信号转换为频域信号，另一个是合成时域信号。

• 将时域信号转换为频域信号

　　代码来源于http://bigsec.net/b52/scipydoc/fft_study.html　　　

　　FFT是将时域信号转换为频域信号，它是对一组数值进行运算，数组长度是2的整数次幂（64，128，256）， 数值可以是实数也可以是复数，通常我们的时域信号都是实数，因此下面都以实数为例。我们可以把这一组实数想像成对某个连续信号按照一定取样周期进行取样而得来，如果对这组N个实数值进行FFT变换，将得到一个有N个复数的数组，我们称此复数数组为频域信号，此复数数组符合如下规律：

1. 下标为0和N/2的两个复数的虚数部分为0，
2. 下标为i和N-i的两个复数共轭，也就是其虚数部分数值相同、符号相反。

　　下面的例子演示了这一个规律，先以rand随机产生有8个元素的实数数组x，然后用fft对其运算之后，观察其结果为8个复数，并且满足上面两个条件：

import  numpy as np
from numpy import *

#随机产生8个数
x = np.random(8)

#对这8个数进行傅里叶变换
xf = np.fft.fft(x)
# (3.988037788578344+0.0j)
# (-0.4137886303518952+0.4932605470110098j)
# (1.2456400001700039+0.14530526335520622j)
# (0.35597667913863856+0.3148093703101355j)
# (0.8683347993093808+0.0j)
# (0.35597667913863856-0.3148093703101355j)
# (1.2456400001700039-0.14530526335520622j)
# (-0.4137886303518952-0.4932605470110098j)

#对xf进行逆傅里叶变换,逆变换之后，实数部分与原来的X相同
xff = np.fft.ifft(xf)

　　结果分析：下标为0的实数表示时域信号中直流成分是多少，下标为i的a+b * j表示时域信号中周期为N/i个取样值的正弦波和余弦波的成分的多少， 其中a表示cos波形的成分，b表示sin波形的成分。用全是1的数组来做实验。

x = np.ones(8)
#array([1., 1., 1., 1., 1., 1., 1., 1.])
np.fft.fft(x)
#[8.+0.j 0.-0.j 0.+0.j 0.+0.j 0.+0.j 0.-0.j 0.-0.j 0.+0.j]

取一个 周期为8个的取样的正弦波，观察FFT结果

x = np.arange(0, 2*np.pi, 2*np.pi/8)
#array([0.        , 0.78539816, 1.57079633, 2.35619449, 3.14159265,
#       3.92699082, 4.71238898, 5.49778714])
y = np.sin(x)
np.fft.fft(y)
#array([ 1.22464680e-16+0.00000000e+00j, -4.36483172e-16-4.00000000e+00j,
#        1.22464680e-16-2.22044605e-16j,  1.91553812e-16-4.44089210e-16j,
#        1.22464680e-16+0.00000000e+00j,  1.91553812e-16+4.44089210e-16j,
#        1.22464680e-16+2.22044605e-16j, -4.36483172e-16+4.00000000e+00j])

　　用linspace创建取样点x，等分数据时步长只能使用整数

#若步长为8，则会7等分，因此设步长为9，将数据8等分，然后省去最后一个点。
x = np.linspace(0, 2*np.pi, 9, endpoint=False)
y = np.cos(x)

np.fft.fft(np.cos(x))/len(x)
#([-8.63506797e-17+0.00000000e+00j,  5.00000000e-01-1.51531594e-16j,
#        3.77494957e-17-9.83914667e-19j,  6.16790569e-18+1.06831260e-17j,
#       -3.77494957e-17-4.17485895e-17j, -3.77494957e-17+4.17485895e-17j,
#        6.16790569e-18-1.06831260e-17j,  3.77494957e-17+9.83914667e-19j,
#        5.00000000e-01+1.51531594e-16j])
#可看出实数的有效值是下标为1的数，5.00000000e-01-1.51531594e-16j，和余弦波之间的关系是0.5 * 2 = 1

　　再取不同的放大倍数作比较。

#将正弦的放大倍数设为2倍
np.fft.fft(2*np.sin(2*x))/len(x)

#array([ 2.46716228e-16+0.00000000e+00j,  2.46716228e-17+1.97372982e-16j,
#       -3.37020635e-16-1.00000000e+00j,  9.86864911e-17-8.54650083e-17j,
#        9.03044069e-17+0.00000000e+00j,  9.03044069e-17-0.00000000e+00j,
#        9.86864911e-17+8.54650083e-17j, -3.37020635e-16+1.00000000e+00j,
#        2.46716228e-17-1.97372982e-16j])

#可看出有效值在下标为2处，放大系数为2，由2*数值= 放大系数可知正弦对应的复数部分数值为-1.

np.fft.fft(0.8*np.cos(2*x))/len(x)

#array([-5.24271984e-17+0.00000000e+00j, -2.46716228e-17+9.08065713e-17j,
#        4.00000000e-01-1.76271580e-16j,  6.32210333e-17+2.67078151e-18j,
#        2.46716228e-17+5.34156302e-18j,  2.46716228e-17-5.34156302e-18j,
#        6.32210333e-17-2.67078151e-18j,  4.00000000e-01+1.76271580e-16j,
#       -2.46716228e-17-9.08065713e-17j])

#可看出有效值在下标为2处，放大系数为0.8，由2*数值= 放大系数可知正弦对应的复数部分数值为0.4，即4.00000000e-01-1.76271580e-16j。

　　接下来考虑正弦波和余弦波叠之后，可产生同频率不同相位的各种余弦波。复数的模代表余弦波的振幅，幅角代表此频率余弦波的相位。

x = np.arange(0, 2*np.pi, 2*np.pi/128)
y = 0.3*np.cos(x) + 0.5*np.cos(2*x+np.pi/4) + 0.8*np.cos(3*x-np.pi/3)
yf = np.fft.fft(y)/len(y)
#前5个数值为有效值
yf[:4]
#计算数值对应的相位角
np.angle(yf[1])

#abs：返回绝对值，np.rad2deg：从弧度转为角度
np.abs(yf[1]), np.rad2deg(np.angle(yf[1]))
# (0.15000000000000002, -5.300924469105861e-15)
# 角度是0度，振幅是0.3
np.abs(yf[2]), np.rad2deg(np.angle(yf[2]))
#(0.2500000000000001, 45.000000000000014)
# 角度是45度，振幅是0.5
np.abs(yf[3]), np.rad2deg(np.angle(yf[3]))
#(0.4, -60.00000000000001)
# 角度是-60度，振幅是0.4

　　也就是说，进行傅里叶变换后，绝对值 *  2 对应振幅，np.rad2deg可求出对应的角度，即相位。

• 合成时域信号

　　使用正弦波和方波去逐步逼近曲线

import numpy as np
import pylab as pl

# 取FFT计算的结果freqs中的前n项进行合成，返回合成结果，计算loops个周期的波形，返回合成波形
def fft_combine(freqs, n, loops=1):
    length = len(freqs) * loops
    data = np.zeros(length)
    index = loops * np.arange(0, length, 1.0) / length * (2 * np.pi)
    for k, p in enumerate(freqs[:n]):
        if k != 0: p *= 2 # 除去直流成分之外，其余的系数都*2
        data += np.real(p) * np.cos(k*index) # 余弦成分的系数为实数部
        data -= np.imag(p) * np.sin(k*index) # 正弦成分的系数为负的虚数部
    return index, data    

# 产生size点取样的三角波，其周期为1
#def triangle_wave(size):
#    x = np.arange(0, 1, 1.0/size)
#    y = np.where(x<0.5, x, 0)
#    y = np.where(x>=0.5, 1-x, y)
#    return x, y

# 产生size点取样的方波，其周期为1
def square_wave(size):
    x = np.arange(0, 1, 1.0/size)
    y = np.where(x<0.5, 1.0, 0)
    return x, y

fft_size = 256

# 计算方波和其FFT
x, y = square_wave(fft_size)
fy = np.fft.fft(y) / fft_size

# 绘制三角波的FFT的前20项的振幅，由于不含下标为偶数的值均为0， 因此取
# log之后无穷小，无法绘图，用np.clip函数设置数组值的上下限，保证绘图正确
pl.figure()
#np.clip(x,3,8):给数值设定范围，对于小于3的数，全部变成3，大于8的数全部变成8
pl.plot(np.clip(20*np.log10(np.abs(fy[:20])), -120, 120), "o")
pl.xlabel("frequency bin")
pl.ylabel("power(dB)")
pl.title("FFT result of triangle wave")

# 绘制原始的三角波和用正弦波逐级合成的结果，使用取样点为x轴坐标
pl.figure()
pl.plot(y, label="original triangle", linewidth=2)
for i in [0,1,3,5,7,9]:
    index, data = fft_combine(fy, i+1, 2)  # 计算两个周期的合成波形
    pl.plot(data, label = "N=%s" % i)
pl.legend()
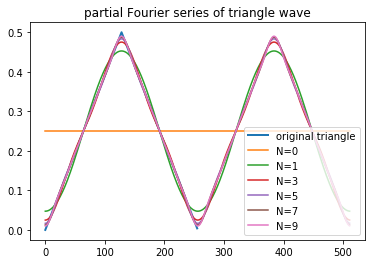
pl.title("partial Fourier series of triangle wave")
pl.show()

用正弦波去逼近方波结果如下所示：

用正弦波去逼近三角波如下所示：