零基础入门深度学习(6) - 长短时记忆网络(LSTM)

---

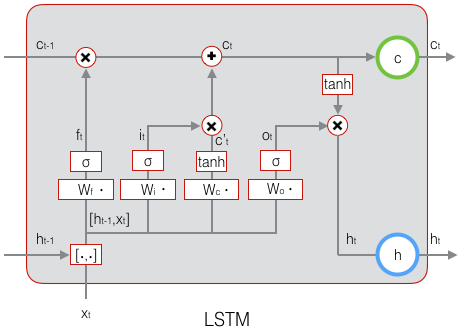
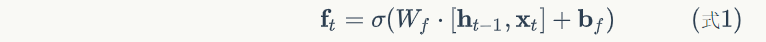
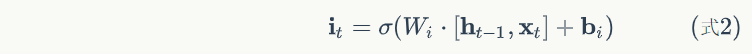
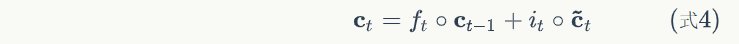
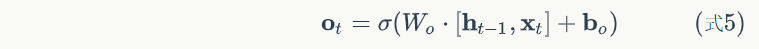
代码：

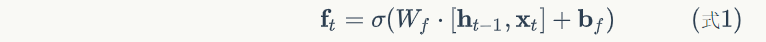
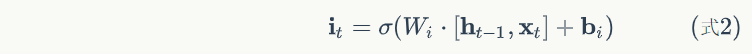
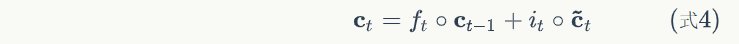
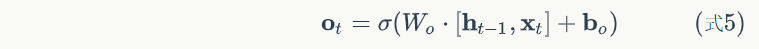
    def forward(self, x):
        '''
        根据式1-式6进行前向计算
        '''
        self.times += 1
        # 遗忘门
        fg = self.calc_gate(x, self.Wfx, self.Wfh,
                            self.bf, self.gate_activator)
        self.f_list.append(fg)
        # 输入门
        ig = self.calc_gate(x, self.Wix, self.Wih,
                            self.bi, self.gate_activator)
        self.i_list.append(ig)
        # 输出门
        og = self.calc_gate(x, self.Wox, self.Woh,
                            self.bo, self.gate_activator)
        self.o_list.append(og)
        # 即时状态
        ct = self.calc_gate(x, self.Wcx, self.Wch,
                            self.bc, self.output_activator)
        self.ct_list.append(ct)
        # 单元状态
        c = fg * self.c_list[self.times - 1] + ig * ct
        self.c_list.append(c)
        # 输出
        h = og * self.output_activator.forward(c)
        self.h_list.append(h)

    def calc_gate(self, x, Wx, Wh, b, activator):
        '''
        计算门
        '''
        h = self.h_list[self.times - 1]  # 上次的LSTM输出
        net = np.dot(Wh, h) + np.dot(Wx, x) + b
        gate = activator.forward(net)
        return gate

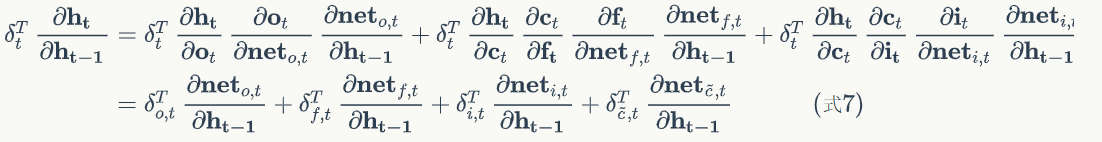
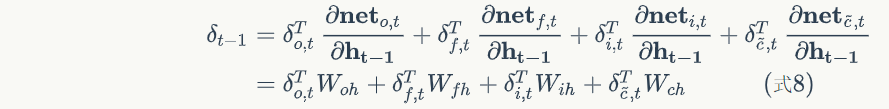
    def calc_delta_k(self, k):
        '''
        根据k时刻的delta_h，计算k时刻的delta_f、
        delta_i、delta_o、delta_ct，以及k-1时刻的delta_h
        '''
        # 获得k时刻前向计算的值
        ig = self.i_list[k]
        og = self.o_list[k]
        fg = self.f_list[k]
        ct = self.ct_list[k]
        c = self.c_list[k]
        c_prev = self.c_list[k - 1]
        tanh_c = self.output_activator.forward(c)
        delta_k = self.delta_h_list[k]

        # 根据式9计算delta_o
        delta_o = (delta_k * tanh_c *
                   self.gate_activator.backward(og))
        delta_f = (delta_k * og *
                   (1 - tanh_c * tanh_c) * c_prev *
                   self.gate_activator.backward(fg))
        delta_i = (delta_k * og *
                   (1 - tanh_c * tanh_c) * ct *
                   self.gate_activator.backward(ig))
        delta_ct = (delta_k * og *
                    (1 - tanh_c * tanh_c) * ig *
                    self.output_activator.backward(ct))
        delta_h_prev = (
                np.dot(delta_o.transpose(), self.Woh) +
                np.dot(delta_i.transpose(), self.Wih) +
                np.dot(delta_f.transpose(), self.Wfh) +
                np.dot(delta_ct.transpose(), self.Wch)
        ).transpose()

        # 保存全部delta值
        self.delta_h_list[k - 1] = delta_h_prev
        self.delta_f_list[k] = delta_f
        self.delta_i_list[k] = delta_i
        self.delta_o_list[k] = delta_o
        self.delta_ct_list[k] = delta_ct

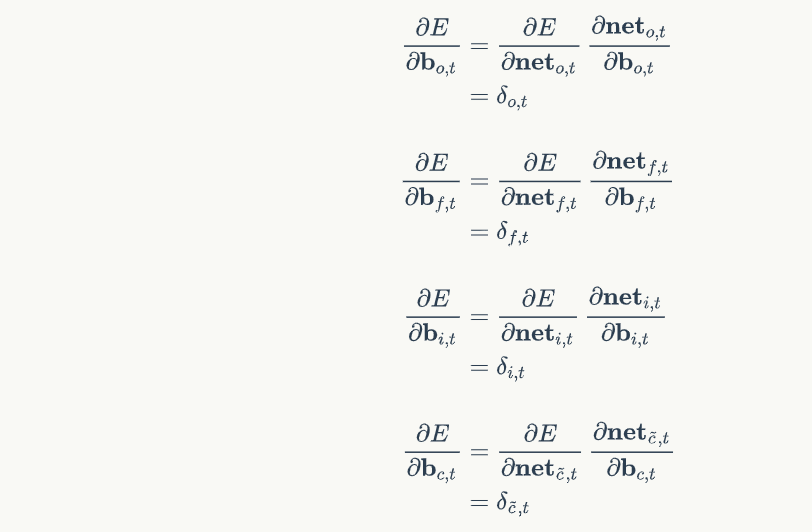
    def calc_gradient_t(self, t):
        '''
        计算每个时刻t权重的梯度
        '''
        h_prev = self.h_list[t - 1].transpose()
        Wfh_grad = np.dot(self.delta_f_list[t], h_prev)
        bf_grad = self.delta_f_list[t]
        Wih_grad = np.dot(self.delta_i_list[t], h_prev)
        bi_grad = self.delta_f_list[t]
        Woh_grad = np.dot(self.delta_o_list[t], h_prev)
        bo_grad = self.delta_f_list[t]
        Wch_grad = np.dot(self.delta_ct_list[t], h_prev)
        bc_grad = self.delta_ct_list[t]
        return Wfh_grad, bf_grad, Wih_grad, bi_grad, \
               Woh_grad, bo_grad, Wch_grad, bc_grad

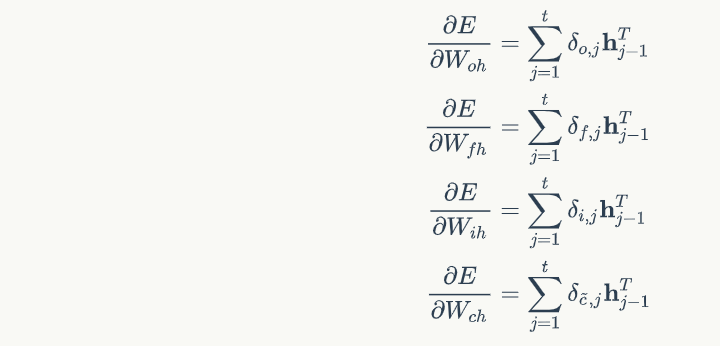
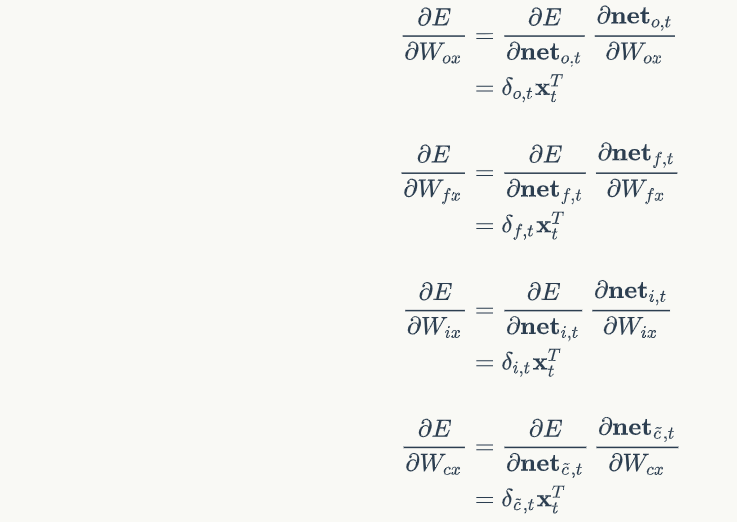
    def calc_gradient(self, x):
        # 初始化遗忘门权重梯度矩阵和偏置项
        self.Wfh_grad, self.Wfx_grad, self.bf_grad = (
            self.init_weight_gradient_mat())
        # 初始化输入门权重梯度矩阵和偏置项
        self.Wih_grad, self.Wix_grad, self.bi_grad = (
            self.init_weight_gradient_mat())
        # 初始化输出门权重梯度矩阵和偏置项
        self.Woh_grad, self.Wox_grad, self.bo_grad = (
            self.init_weight_gradient_mat())
        # 初始化单元状态权重梯度矩阵和偏置项
        self.Wch_grad, self.Wcx_grad, self.bc_grad = (
            self.init_weight_gradient_mat())

        # 计算对上一次输出h的权重梯度
        for t in range(self.times, 0, -1):
            # 计算各个时刻的梯度
            (Wfh_grad, bf_grad,
             Wih_grad, bi_grad,
             Woh_grad, bo_grad,
             Wch_grad, bc_grad) = (
                self.calc_gradient_t(t))
            # 实际梯度是各时刻梯度之和
            self.Wfh_grad += Wfh_grad
            self.bf_grad += bf_grad
            self.Wih_grad += Wih_grad
            self.bi_grad += bi_grad
            self.Woh_grad += Woh_grad
            self.bo_grad += bo_grad
            self.Wch_grad += Wch_grad
            self.bc_grad += bc_grad

        # 计算对本次输入x的权重梯度
        xt = x.transpose()
        self.Wfx_grad = np.dot(self.delta_f_list[-1], xt)
        self.Wix_grad = np.dot(self.delta_i_list[-1], xt)
        self.Wox_grad = np.dot(self.delta_o_list[-1], xt)
        self.Wcx_grad = np.dot(self.delta_ct_list[-1], xt)

参考：

https://zybuluo.com/hanbingtao/note/581764

https://www.cnblogs.com/ratels/p/11416515.html