DBSCAN密度聚类

1. 密度聚类概念

DBSCAN(Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法)是一种很典型的密度聚类算法，和K-Means，BIRCH这些一般只适用于凸样本集的聚类相比，DBSCAN既可以适用于凸样本集，也可以适用于非凸样本集。

2. 密度聚类步骤

DBSCAN算法描述:

输入: 包含n个对象的数据库，半径e，最少数目MinPts;

输出:所有生成的簇，达到密度要求。

(1)Repeat

(2)从数据库中抽出一个未处理的点；

(3)IF抽出的点是核心点 THEN 找出所有从该点密度可达的对象，形成一个簇；

(4)ELSE 抽出的点是边缘点(非核心对象)，跳出本次循环，寻找下一个点；

(5)UNTIL 所有的点都被处理。

DBSCAN对用户定义的参数很敏感，细微的不同都可能导致差别很大的结果，而参数的选择无规律可循，只能靠经验确定。

              

这个算法的关键是理解几个概念：

• 直接密度可达
• 密度可达
• 核心点
• 边界点
• 噪声点

理解这些概念的一个资料：ppt

 

3. python实现

思路：首先找出所有核心点，核心点就是那些在半径e以内的邻域中有>=MinPts个点的点。注意：核心点以内的所有点都与核心点为同一类!  所以如果某两类点集中有一个点为重复，那他们应该合并为一类！举例：类别1：[1,2,4,6,8],类别2：[3,6,7,9,10,99]。这两个集合最初是两个类别，但是因为有共同点6，那么他俩应当合并为1类。所以这个算法就很简单了，代码步骤如下：

1）求出所有点的距离矩阵dis=[n,n], n为数据的个数。

2）如果e取值为3，那么dis的每一行中>3的所有点个数的和只要>MinPts,则为1个类别。 

3）所有这些类别进行重复检查，只要有重复值则合并，直到没有重复。

4）这些没有重复的类别就是最终形成的类别。

简单说明：

 

 

  

代码：

# coding:utf-8
"""
@author = LPS
"""
import numpy as np
import matplotlib.pyplot as plt

data = np.loadtxt('moon.txt')
n,m = data.shape
all_index = np.arange(n)
dis = np.zeros([n,n])
data = np.delete(data, m-1, axis=1)

def dis_vec(a,b):    # 计算两个向量的距离

    if len(a)!=len(b):
        return Exception
    else:
        return np.sqrt(np.sum(np.square(a-b)))

for i in range(n):   # 计算距离矩阵
    for j in range(i):
        dis[i,j] = dis_vec(data[i],data[j])
        dis[j,i] = dis[i,j]

def dbscan(s, minpts):   # 密度聚类

    center_points = []   # 存放最终的聚类结果
    k = 0  # 检验是否进行了合并过程

    for i in range(n):
        if sum(dis[i] <= s) >= minpts:   # 查看距离矩阵的第i行是否满足条件
            if len(center_points) == 0:  # 如果列表长为0，则直接将生成的列表加入
                center_points.append(list(all_index[dis[i] <= s]))
            else:
                for j in range(len(center_points)):   # 查找是否有重复的元素
                    if set(all_index[dis[i] <= s]) & set(center_points[j]):
                        center_points[j].extend(list(all_index[dis[i] <= s]))
                        k=1   # 执行了合并操作
                if k==0 :
                    center_points.append(list(all_index[dis[i] <= s]))  # 没有执行合并说明这个类别单独加入
                k=0

    lenc =  len(center_points)

    # 以下这段代码是进一步查重，center_points中所有的列表并非完全独立，还有很多重复
    # 那么为何上面代码已经查重了，这里还需查重，其实可以将上面的步骤统一放到这里，但是时空复杂的太高
    # 经过第一步查重后，center_points中的元素数目大大减少，此时进行查重更快！
    k = 0
    for i in range(lenc-1):
        for j in range(i+1, lenc):
            if set(center_points[i]) & set(center_points[j]):
                center_points[j].extend(center_points[i])
                center_points[j] = list(set(center_points[j]))
                k=1

        if k == 1:
            center_points[i] = []   # 合并后的列表置空
        k = 0

    center_points = [s for s in center_points if s != []]   # 删掉空列表即为最终结果

    return center_points

if __name__ == '__main__':
    center_points = dbscan(0.2,10)  # 半径和元素数目
    c_n = center_points.__len__()   # 聚类完成后的类别数目
    print (c_n)
    ct_point = []
    color = ['g','r','b','m','k']
    noise_point = np.arange(n)      # 没有参与聚类的点即为噪声点
    for i in range(c_n):
        ct_point = list(set(center_points[i]))
        noise_point = set(noise_point)- set(center_points[i])
        print (ct_point.__len__())   # 输出每一类的点个数
        print (ct_point)             # 输出每一类的点
        print ("**********")

    noise_point = list(noise_point)

    for i in range(c_n):
        ct_point = list(set(center_points[i]))
        plt.scatter(data[ct_point,0], data[ct_point,1], color=color[i])       # 画出不同类别的点
    plt.scatter(data[noise_point,0], data[noise_point,1], color=color[c_n], marker='h', linewidths=0.1)   # 画噪声点
    plt.show()　

DBSCAN的主要优点有：

　　　　1） 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

　　　　2） 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

　　　　3） 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

DBSCAN的主要缺点有：

　　　　1）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

　　　　2） 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。

　　　　3） 调参相对于传统的K-Means之类的聚类算法稍复杂，不同的参数组合对最后的聚类效果有较大影响。

实验：

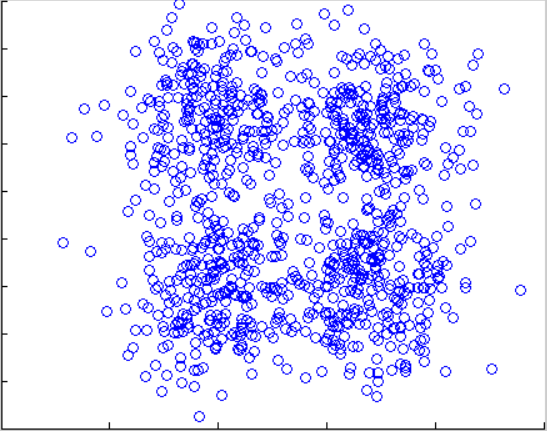
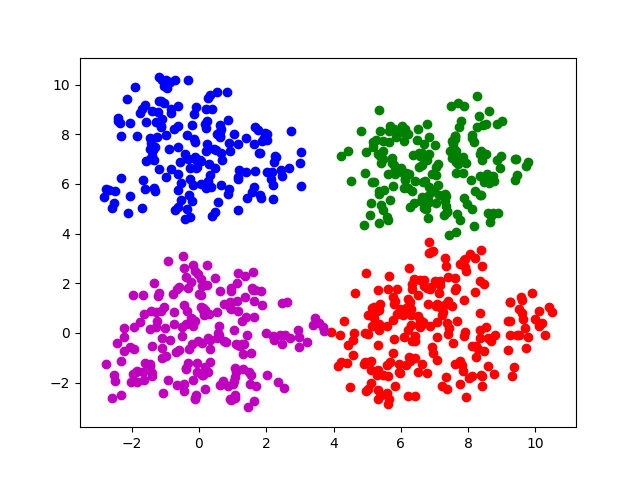
原图                                                   square4  e=0.85  minpts = 13                                            square4-sklearn e=0.9 minpts=15

                       

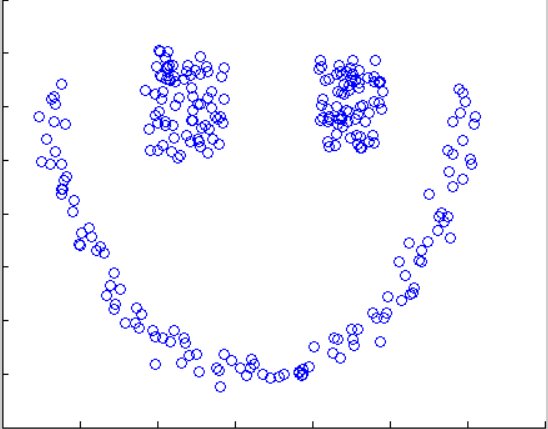
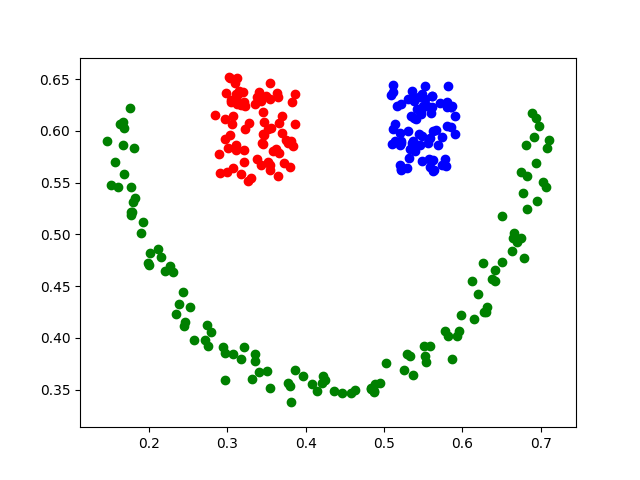
原图                                                                                                                         结果图

  

原图                                                                       square1 1.185，8                                                                square1   0.85 15

         

原图                                                                                            结果图

       

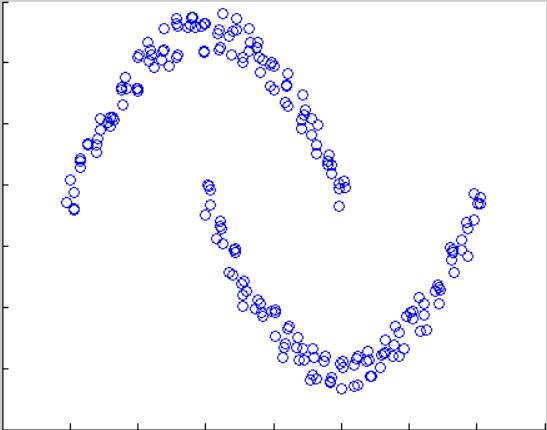
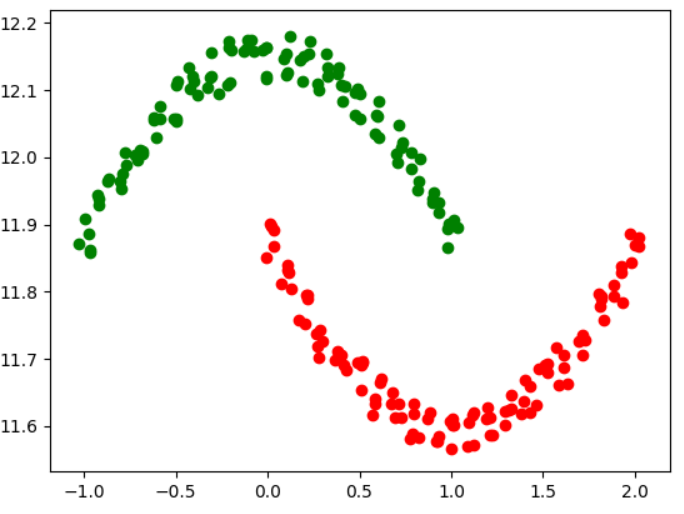
原图                                                                                                                   结果图

实验过程中：前几幅图由于分布比较密集，参数调整要很多次，后几张图因为分布比较分散，所以参数基本一次设置成功。

结果和资料已上传，下载~~~