3d图像识别基础论文：pointNet阅读笔记

PointNet 论文阅读：

主要思路：输入独立的点云数据，进行变换不变性处理（T-net）后，通过pointNet网络训练后，最后通过最大池化和softMax分类器，输出评分结果。

摘要：

相较于之前其他处理点云数据的论文，将数据转换为三维体素网格或者图象集合，pointNet最大的不同是，对于点云数据，会直接进行处理，而非将点云数据进行格式化处理，从而避免了将点云数据格式化后，产生的unnecessarily voluminous以及像素点失真的问题。

点云的问题：

1. 无序。与图像中的像素阵列或体积网格中的体素阵列不同，点云是一组没有特定顺序的点。 换句话说，处理N个3D点集合就会有n！种排列方式。

处理方法：

提出了三种方法:

1）将输入排序为规范的顺序;（对于扰动不稳定）

2）将输入作为一个序列来训练一个RNN，但是用各种排列来增加训练数据; （顺序无法被完全忽视）

3）使用简单的对称函数来汇总每个点的信息。

首先采取mlp提取特征（只有*和+的对称函数）并且采用最大池化函数，导致输出结果不受集合中点的排列顺序影响。

深度网络模拟通用对称函数：

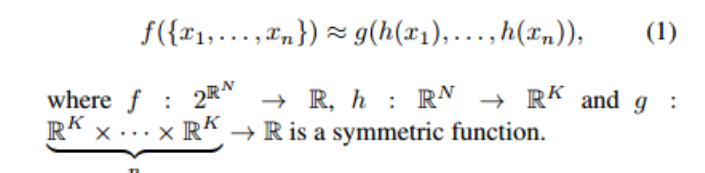
输入总共n个点的无序云图点集（{x1，x2 … , xn}）, 通用函数f 输出该云图分类（汽车，书桌，飞机）。其中h函数用MLP网络模拟：g用最大池化模拟。

2.点之间的相互作用。点来自具有距离度量的空间。这意味着点不是孤立的，相邻点形成一个有意义的子集。 因此，该模型需要能够从附近的点捕获局部结构，以及局部结构之间的组合相互作用。分割和语义分析需要考虑到点之间的相互作用。

处理方法：在分割网络中，将局部特征和全局特征连接，并进行进一步的特征提取，最终提取的结果与局部和全局特征相关。

3.变换下的不变性。 作为一个几何对象，点集的学习表示对某些变换应该是不变的。 例如，旋转点和平移点不应该修改全局点云类别或点的分割。对于一个3D图像，当我们进行例如旋转、上移等操作时，不论是目标分类还是部分分割，都应保证其结果不变。

处理方法：论文作者提出了在进行特征提取之前，先对点云数据进行对齐的方式来保证不变性。对齐操作是通过训练一个小型的网络（T-net，类似于大型网络，由点独立特征提取，最大池化和全连接层的基本模块组成）来得到转换矩阵，并将之和输入点云数据相乘来实现.相当于在数据预处理阶段直接进行处理，保证其后的结果不变性。

4.点云具有稀疏性（信息点提取）。

处理方法：网络高效地学习一组优化功能/标准，选择点云的信息点，并对其选择原因进行编码。

方法：

1. 网络分析：

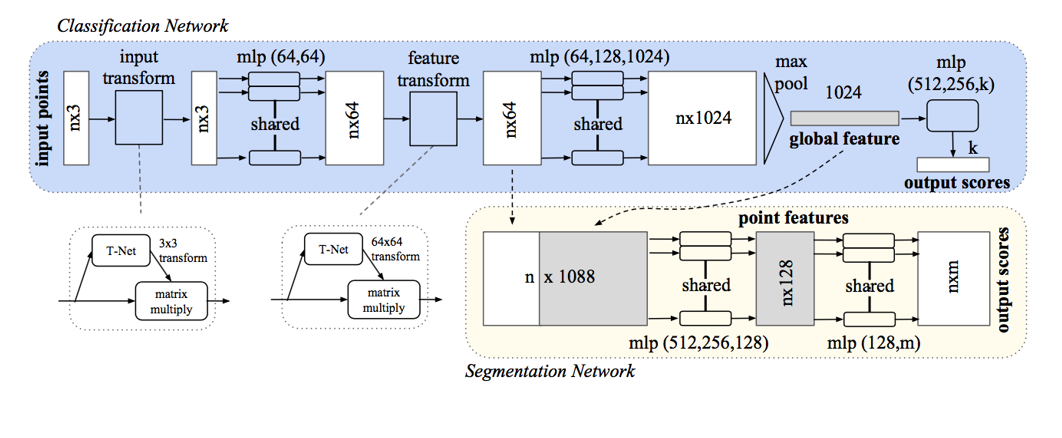
1.三个初始纬度。 2.T-net对齐处理 3.最大池化合并特征，解决无序性 4.连接全局和局部特征 4.softmax分类器

1. 两个定理：

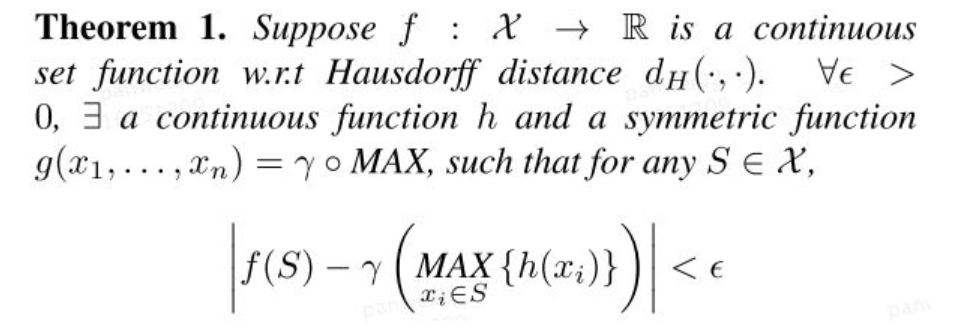
和神经网络一样，该网络也可以拟合任意的连续集合函数。

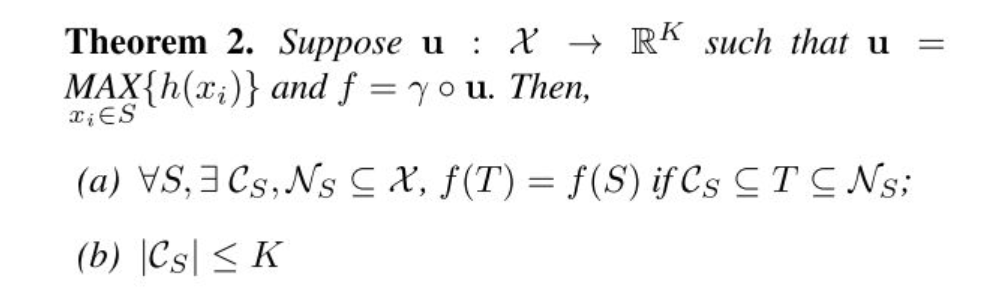
对噪声和缺失的鲁棒性。

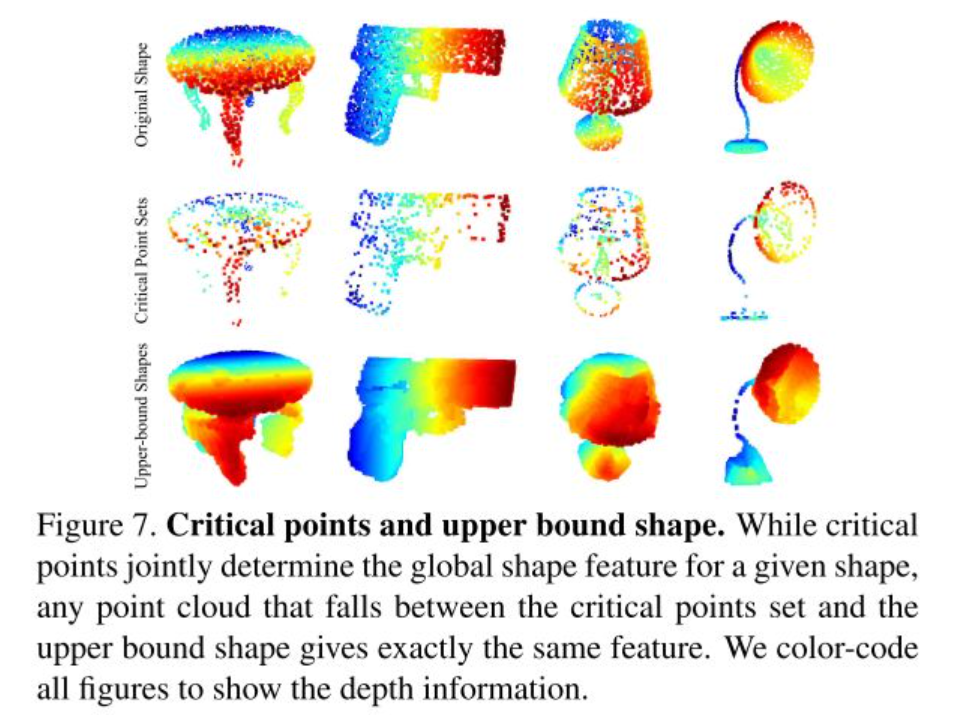
创新点：

1. 对称函数处理无序性处理。
2. t-net微型网络进行变换不变性处理。
3. 全局变量和局部变量合并处理相关性。

应用：神经网络对于无序的信息点的处理。

问题：

1.正则项：相较于前一个3 * 3变换矩阵，后面的变换矩阵为64 * 64 = 4096，由于变换矩阵过大，通过添加正则项，使变换矩阵近似于正交矩阵，此时所需要的参数将大大减少。

2.T-net网络实现的细节：（如何具体实现对齐和变换不变性）。

3.两个定理的证明过程。