v-show 和 v-if 对 v-chart的影响
借鉴:https://blog.csdn.net/xiaxiangyun/article/details/78909991
使用v-show控制tab切换
其中一个tab数据请求后显示第二个tab,第二个tab有v-chart 饼图和柱状图,打印出来已经请求的到数据,但是由于先执行v-show :display:none,v-chart没有拿到正确的宽高
这时用v-if即可解决问题
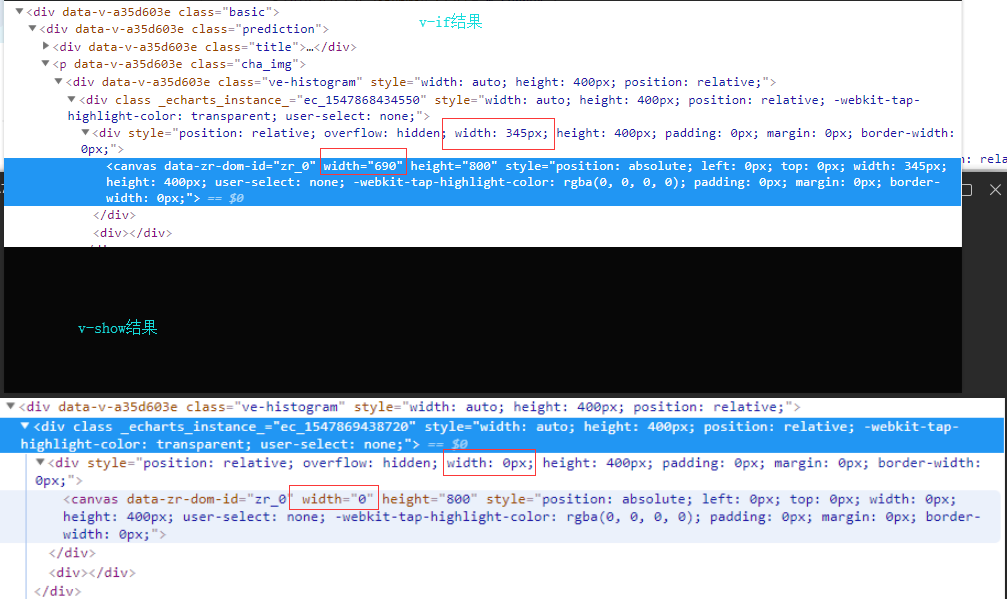
v-show 和 v-if 对 v-chart的影响的更多相关文章
- SIP模块版本错误问题:the sip module implements API v??? but XXX module requires API v???
系统安装了python 2.7,继续安装PyQt4,于是依次下载sip.pyqt4源码进行安装.用以下代码测试: import PyQt4.QtGui 显示出错.错误信息:the sip module ...
- n维向量空间W中有子空间U,V,如果dim(U)=r dim(V)=n-r U交V !={0},那么U,V的任意2组基向量的组合必定线性相关
如题取U交V中的向量p (p!=0), 那么p可以由 U中的某一组基线性组合成(系数不全是零),同时,-p也可以由V中的某一组基线性组合成(系数不全为零) 考察p+(-p)=0 可知道,U中的这组基跟 ...
- XV Open Cup named after E.V. Pankratiev. GP of Tatarstan
A. Survival Route 留坑. B. Dispersed parentheses $f[i][j][k]$表示长度为$i$,未匹配的左括号数为$j$,最多的未匹配左括号数为$k$的方案数. ...
- XVII Open Cup named after E.V. Pankratiev. GP of SPb
A. Array Factory 将下标按前缀和排序,然后双指针,维护最大的右边界即可. #include<cstdio> #include<algorithm> using ...
- XVI Open Cup named after E.V. Pankratiev. GP of Ukraine
A. Associated Vertices 首先求出SCC然后缩点,第一次求出每个点能到的点集,第二次收集这些点集即可,用bitset加速,时间复杂度$O(\frac{nm}{64})$. #inc ...
- XVI Open Cup named after E.V. Pankratiev. GP of Peterhof
A. (a, b)-Tower 当指数大于模数的时候用欧拉定理递归计算,否则直接暴力计算. #include<cstdio> #include<algorithm> #incl ...
- XVI Open Cup named after E.V. Pankratiev. GP of Siberia
A. Passage 枚举两个点,看看删掉之后剩下的图是否是二分图. #include <bits/stdc++.h> using namespace std ; const int MA ...
- XVI Open Cup named after E.V. Pankratiev. GP of Ekaterinburg
A. Avengers, The 留坑. B. Black Widow 将所有数的所有约数插入set,然后求mex. #include<bits/stdc++.h> using names ...
- XVI Open Cup named after E.V. Pankratiev. GP of Eurasia
A. Nanoassembly 首先用叉积判断是否在指定向量右侧,然后解出法线与给定直线的交点,再关于交点对称即可. #include<bits/stdc++.h> using names ...
- XVI Open Cup named after E.V. Pankratiev. GP of SPB
A. Bubbles 枚举两个点,求出垂直平分线与$x$轴的交点,答案=交点数+1. 时间复杂度$O(n^2\log n)$. #include<cstdio> #include<a ...
随机推荐
- [Python] pip 简明指南
安装 1. 使用 apt 安装: $ sudo apt-get install python-pip 截止本文落笔,apt 安装 pip 版本为 1.0,但 pip 最新发行版本为 1.5.6 $ p ...
- 131、ThreadLocal (转载)
http://blog.csdn.net/lufeng20/article/details/24314381 http://baike.baidu.com/link?url=7eL0qQm_5ULls ...
- 《转载》spring定时任务详解(@Scheduled注解)
本文转载自爱如指间沙 //每一个小时执行一次 @Scheduled(cron = "0 0 * * * ?") public void saveDailyScoreSchedule ...
- Http 调用netty 服务,服务调用客户端,伪同步响应.ProtoBuf 解决粘包,半包问题.
实际情况是: 公司需要开发一个接口给新产品使用,需求如下 1.有一款硬件设备,客户用usb接上电脑就可以,但是此设备功能比较单一,所以开发一个服务器程序,辅助此设备业务功能 2.解决方案,使用Sock ...
- 搞懂MapReduce
MapReduce的主要思想就是将计算任务分发至多台计算机(slave),然后master综合计算机结果.所以就涉及到多台计算机通信和同步的问题,这个应该由hadoop完成,把环境配置好后就像单机操作 ...
- 试着理解cookie和session
web服务一个特点是提供个性化服务,为很多客户端提供服务,那么每个用户不同,服务自然不同,所以要记住用户及其状态,这也很多应用软件的通用功能. 由于http是无状态的,Session和Cookie是两 ...
- 如何实现@ResponseBody,把Json字符串转换为指定类型
1.问题 spring 是如何把 http中的body,转换为指定类的,里面的难点其实在于泛型的处理. 2.Spring的处理 2.1 HandlerMethod 这个类Spring对Method的封 ...
- vins-mono源码解读
https://blog.csdn.net/q597967420/article/details/76099409
- [No000010D]Git6/9-分支管理
分支就是科幻电影里面的平行宇宙,当你正在电脑前努力学习Git的时候,另一个你正在另一个平行宇宙里努力学习SVN. 如果两个平行宇宙互不干扰,那对现在的你也没啥影响.不过,在某个时间点,两个平行宇宙合并 ...
- [No0000ED]IPSec策略之管理
IP安全策略 @echo off :again set num= set ippolicyname= set ismmpfs= set keytime= set keyexpress= set new ...
