局部加权线性回归(Locally weighted linear regression)
首先我们来看一个线性回归的问题,在下面的例子中,我们选取不同维度的特征来对我们的数据进行拟合。
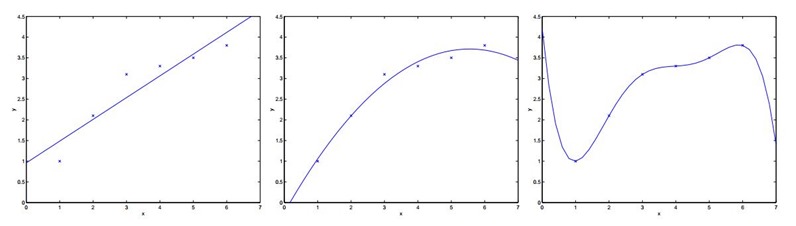
对于上面三个图像做如下解释:
选取一个特征 ,
, 来拟合数据,可以看出来拟合情况并不是很好,有些数据误差还是比较大
来拟合数据,可以看出来拟合情况并不是很好,有些数据误差还是比较大
针对第一个,我们增加了额外的特征 ,
, ,这时我们可以看出情况就好了很多。
,这时我们可以看出情况就好了很多。
这个时候可能有疑问,是不是特征选取的越多越好,维度越高越好呢?所以针对这个疑问,如最右边图,我们用5揭多项式使得数据点都在同一条曲线上,为 。此时它对于训练集来说做到了很好的拟合效果,但是,我们不认为它是一个好的假设,因为它不能够做到更好的预测。
。此时它对于训练集来说做到了很好的拟合效果,但是,我们不认为它是一个好的假设,因为它不能够做到更好的预测。
针对上面的分析,我们认为第二个是一个很好的假设,而第一个图我们称之为欠拟合(underfitting),而最右边的情况我们称之为过拟合(overfitting)
所以我们知道特征的选择对于学习算法的性能来说非常重要,所以现在我们要引入局部加权线性回归,它使得特征的选择对于算法来说没那么重要,也就是更随性了。
在我们原始的线性回归中,对于输入变量 ,我们要预测,通常要做:
,我们要预测,通常要做:
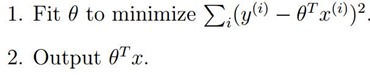
而对于局部加权线性回归来说,我们要做:
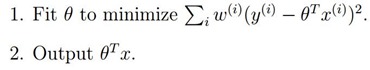
 为权值,从上面我们可以看出,如果
为权值,从上面我们可以看出,如果 很大,我们将很难去使得
很大,我们将很难去使得 小,所以如果
小,所以如果 很小,则它所产生的影响也就很小。
很小,则它所产生的影响也就很小。
通常我们选择 的形式如下所示:
的形式如下所示:
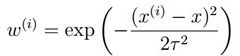
上式中参数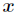 为新预测的样本特征数据,它是一个向量,参数
为新预测的样本特征数据,它是一个向量,参数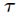 控制了权值变化的速率,
控制了权值变化的速率, 和
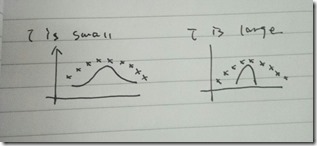
和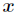 的图像如下
的图像如下
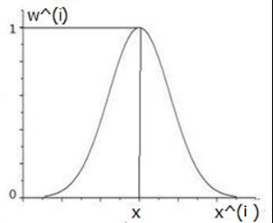
可以看到
(1)如果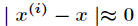 ,则
,则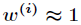 。
。
(2)如果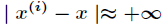 ,则
,则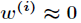 。
。
也即,离 很近的样本,权值接近于1,而对于离
很近的样本,权值接近于1,而对于离 很远的样本,此时权值接近于0,这样就是在
很远的样本,此时权值接近于0,这样就是在 局部构成线性回归,它依赖的也只是
局部构成线性回归,它依赖的也只是 周边的点
周边的点
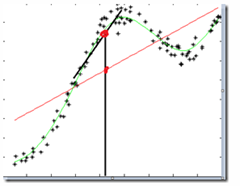
图中红色直线使用线性回归做的结果,黑色直线使用LWR做的结果,可以看到局部加权回归的效果较好。
注意:
的形式跟高斯函数很像,但是它和高斯函数一点关系都没有,
是波长参数,
越大远距离样本权值下降更快。
局部加权回归在每一次预测新样本时都会重新的确定参数,从而达到更好的预测效果当数据规模比较大的时候计算量很大,学习效率很低。并且局部加权回归也不是一定就是避免underfitting。
对于线性回归算法,一旦拟合出适合训练数据的参数θi’s,保存这些参数θi’s,对于之后的预测,不需要再使用原始训练数据集,所以是参数学习算法。
对于局部加权线性回归算法,每次进行预测都需要全部的训练数据(每次进行的预测得到不同的参数θi’s),没有固定的参数θi’s,所以是非参数算法。
局部加权线性回归(Locally weighted linear regression)的更多相关文章
- 局部权重线性回归(Locally weighted linear regression)
在线性回归中,因为对參数个数选择的问题是在问题求解之前已经确定好的,因此參数的个数不能非常好的确定,假设參数个数过少可能拟合度不好,产生欠拟合(underfitting)问题,或者參数过多,使得函数过 ...
- Locally weighted linear regression(局部加权线性回归)
(整理自AndrewNG的课件,转载请注明.整理者:华科小涛@http://www.cnblogs.com/hust-ghtao/) 前面几篇博客主要介绍了线性回归的学习算法,那么它有什么不足的地方么 ...
- Locally Weighted Linear Regression 局部加权线性回归-R实现
局部加权线性回归 [转载时请注明来源]:http://www.cnblogs.com/runner-ljt/ Ljt 作为一个初学者,水平有限,欢迎交流指正. 线性回归容易出现过拟合或欠拟合的问 ...
- 局部加权回归、欠拟合、过拟合(Locally Weighted Linear Regression、Underfitting、Overfitting)
欠拟合.过拟合 如下图中三个拟合模型.第一个是一个线性模型,对训练数据拟合不够好,损失函数取值较大.如图中第二个模型,如果我们在线性模型上加一个新特征项,拟合结果就会好一些.图中第三个是一个包含5阶多 ...
- 线性回归(最小二乘法、批量梯度下降法、随机梯度下降法、局部加权线性回归) C++
We turn next to the task of finding a weight vector w which minimizes the chosen function E(w). Beca ...
- 线性回归模型(Linear Regression)及Python实现
线性回归模型(Linear Regression)及Python实现 http://www.cnblogs.com/sumai 1.模型 对于一份数据,它有两个变量,分别是Petal.Width和Se ...
- 贝叶斯线性回归(Bayesian Linear Regression)
贝叶斯线性回归(Bayesian Linear Regression) 2016年06月21日 09:50:40 Duanxx 阅读数 54254更多 分类专栏: 监督学习 版权声明:本文为博主原 ...
- 机器学习:线性回归法(Linear Regression)
# 注:使用线性回归算法的前提是,假设数据存在线性关系,如果最后求得的准确度R < 0,则说明很可能数据间不存在任何线性关系(也可能是算法中间出现错误),此时就要检查算法或者考虑使用其它算法: ...
- matlab练习程序(局部加权线性回归)
通常我们使用的最小二乘都需要预先设定一个模型,然后通过最小二乘方法解出模型的系数. 而大多数情况是我们是不知道这个模型的,比如这篇博客中z=ax^2+by^2+cxy+dx+ey+f 这样的模型. 局 ...
随机推荐
- azure 架构选择
在azure中主要有以下3种不同的托管环境. 平台即服务(PaaS)提供了可管理的托管环境,可以直接部署应用而不需要关心背后的虚拟机和网络资源.例如,当需要托管一个应用时,只需要指定实例的个数,azu ...
- MacDown语法
markdown编辑器太多,作为新手比较容易MacDown 相对容易上手,切使用简单方便,满足一般需求 下载地址:http://macdown.uranusjr.com/ ## 标题 # 一级标题 # ...
- 在crontab中执行shell脚本的问题
crontab中记录的编写比较简单,下面是一个示例: * * * /app/tpssapp/ftpsrc/tools/statTables/statTables.sh > /app/tpssap ...
- HDU - 5628:Clarke and math (组合数&线性筛||迪利克雷卷积)
题意:略. 思路:网上是用卷积或者做的,不太会. 因为上一题莫比乌斯有个类似的部分,所以想到了每个素因子单独考虑. 我们用C(x^p)表示p次减少分布在K次减少里的方案数,由隔板法可知,C(x^p)= ...
- 使用python处理selenium中的css_selector定位元素的模糊匹配问题
# 匹配id,先指定一个html标签,然后加上“#”符号,再加上id的属性值 self.driver.find_element_by_css_selector('div#ID').click() # ...
- Java8中计算日期时间差
一.简述 在Java8中,我们可以使用以下类来计算日期时间差异: 1.Period 2.Duration 3.ChronoUnit 二.Period类 主要是Period类方法getYears(),g ...
- css 2D动画
2D动画: 通过 CSS3 transform转换,我们能够对元素进行移动.缩放.转动.拉长或拉伸. 2D移动:translate().使用translate()函数,你可以把元素从原来的位置移动. ...
- js核心知识
枚举属性: var o = {x:1} console.log("x" in o);//true console.log("toString" in o);// ...
- 【转】VC 模式对话框和非模式对话框的创建,销毁和区别
原文网址:http://blog.csdn.net/mycaibo/article/details/6002151 VC 模式对话框和非模式对话框的创建,销毁和区别 在WIN32中,模式对话框的创 ...
- 一篇文章学LINQ(原创)
本篇文章主要介绍linq的基本用法,采用sql和linq比较的方式由浅入深进行学习, 注意:此文章是根据真实表来进行案例说明,表结构如下: 表1: Student(学生表) ...
