Count on a tree（SPOJ COT + 树上第k大 + 主席树 + LCA）

题目链接：https://www.spoj.com/problems/COT/en/

题目：

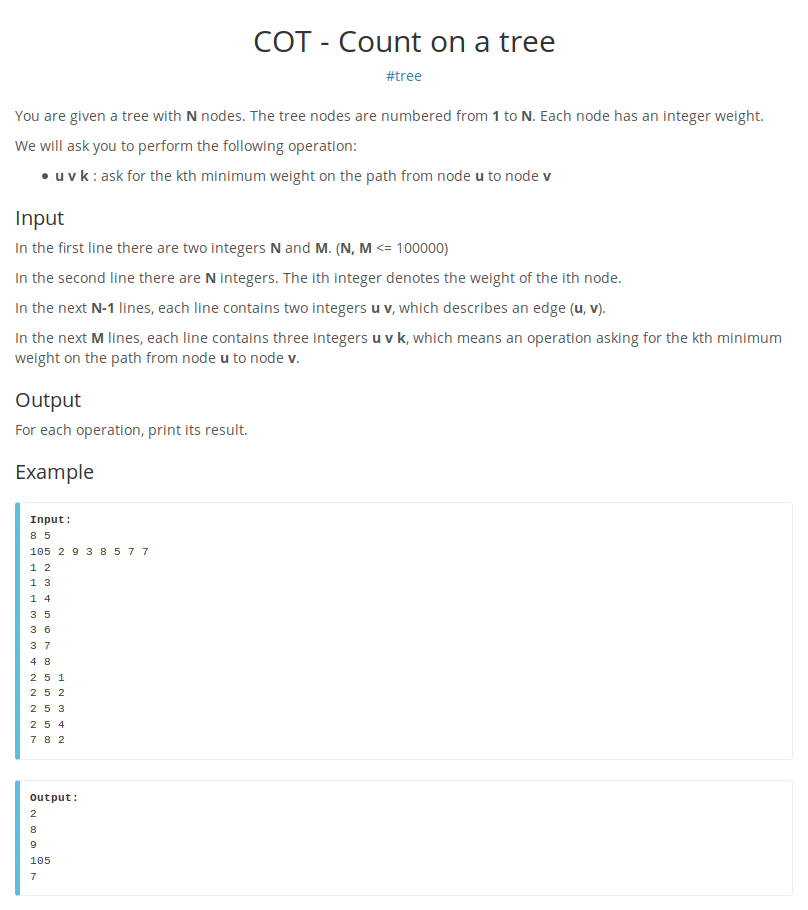
题意：

　　给你一棵有n个节点的树，求节点u到节点v这条链上的第k大。

思路：

　　我们首先用dfs进行建题目给的树，然后在dfs时进行主席树的update操作。众所周知，主席树采用的是前缀和思想，区间第k大是与前一个树添加新的线段树，而树上第k大则是与父亲节点添加新的线段树，因而在此思想上此题的答案为sum[u] + sum[v] - sum[lca(u,v)] - sum[fa[lca(u,v)]。求第k大操作和区间第k大一样，就不描述了～

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <ctime>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long LL;
 typedef pair<LL, LL> pLL;
 typedef pair<LL, int> pli;
 typedef pair<int, LL> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long uLL;

 #define lson rt<<1
 #define rson rt<<1|1
 #define lowbit(x) x&(-x)
 #define name2str(name) (#name)
 #define bug printf("*********\n");
 #define debug(x) cout<<#x"=["<<x<<"]" <<endl;
 #define FIN freopen("/home/dillonh/CLionProjects//in.txt", "r", stdin);
 #define FOUT freopen("D://code//out.txt", "w", stdout);
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = ;
 const int maxn =  + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const LL INF = 0x3f3f3f3f3f3f3f3fLL;

 int n, q, tot, cnt, x, y, k, len;
 int head[maxn], root[maxn];
 int a[maxn], deep[maxn], fa[maxn][];
 vector<int> v;

 struct edge {
     int v, next;
 }ed[maxn<<];

 void addedge(int u, int v) {
     ed[tot].v = v;
     ed[tot].next = head[u];
     head[u] = tot++;
     ed[tot].v = u;
     ed[tot].next = head[v];
     head[v] = tot++;
 }

 struct node {
     int l, r, sum;
 }tree[maxn*];

 int getid(int x) {
     return lower_bound(v.begin(), v.end(), x) - v.begin() + ;
 }

 void update(int l, int r, int& x, int y, int pos) {
     tree[++cnt] = tree[y], tree[cnt].sum++, x = cnt;
     if(l == r) return;
     int mid = (l + r) >> ;
     if(mid >= pos) update(l, mid, tree[x].l, tree[y].l, pos);
     else update(mid + , r, tree[x].r, tree[y].r, pos);
 }

 int query(int l, int r, int x, int y, int p, int pp, int k) {
     if(l == r) return l;
     int mid = (l + r) >> ;
     int sum = tree[tree[x].l].sum + tree[tree[y].l].sum - tree[tree[p].l].sum - tree[tree[pp].l].sum;
     if(sum >= k) return query(l, mid, tree[x].l, tree[y].l, tree[p].l, tree[pp].l, k);
     else return query(mid + , r, tree[x].r, tree[y].r, tree[p].r, tree[pp].r, k - sum);
 }

 void dfs(int u, int d, int p) {
     deep[u] = d;
     fa[u][] = p;
     update(, len, root[u], root[p], getid(a[u]));
     for(int i = head[u]; ~i; i = ed[i].next) {
         int v = ed[i].v;
         if(v != p) {
             dfs(v, d + , u);
         }
     }
 }

 void lca() {
     for(int i = ; i <= n; i++) {
         for(int j = ; ( << j) <= n; j++) {
             fa[i][j] = -;
         }
     }
     for(int j = ; ( << j) <= n; j++) {
         for(int i = ; i <= n; i++) {
             if(fa[i][j-] != -) {
                 fa[i][j] = fa[fa[i][j-]][j-];
             }
         }
     }
 }

 int cal(int u, int v) {
     if(deep[u] < deep[v]) swap(u, v);
     int k;
     for(k = ; ( << ( + k)) <= deep[u]; k++);
     for(int i = k; i >= ; i--) {
         if(deep[u] - ( << i) >= deep[v]) {
             u = fa[u][i];
         }
     }
     if(u == v) return u;
     for(int i = k; i >= ; i--) {
         if(fa[u][i] != - && fa[u][i] != fa[v][i]) {
             u = fa[u][i];
             v = fa[v][i];
         }
     }
     return fa[u][];
 }

 int main() {
 #ifndef ONLINE_JUDGE
     FIN;
 #endif
     scanf("%d%d", &n, &q);
     memset(head, -, sizeof(head));
     for(int i = ; i <= n; i++) scanf("%d", &a[i]), v.push_back(a[i]);
     sort(v.begin(), v.end());
     v.erase(unique(v.begin(), v.end()), v.end());
     len = v.size();
     for(int i = ; i < n; i++) scanf("%d%d", &x, &y), addedge(x, y);
     dfs(, , );
     lca();
     while(q--) {
         scanf("%d%d%d", &x, &y, &k);
         int p = cal(x, y);
         printf("%d\n", v[query(, len, root[x], root[y], root[p], root[fa[p][]], k)-]);
     }
     return ;
 }