[CF1043G]Speckled Band

题意：给定字符串$s_{1\cdots n}$，多次询问它的一个子串$s_{l\cdots r}$能否被切割成多个部分，使得至少有一个部分出现两次，且切出来的本质不同字符串数最少

做一道题学了两个算法...

首先是一个找出所有形如$aa$的子串的算法，来自于这篇论文，好像没有名字？那就叫它main and lorentz算法吧...

整个算法基于分治，每次找出跨越$s_{l\cdots mid},s_{mid+1\cdots r}$的那些$aa$串，不妨先找那些对称轴在右边的$aa$串，之后反过来找即可

我们要找连接$u,v$两个串后新形成的对称轴在$v$内的$aa$串，先用扩展kmp预处理出$ls_i=\left\lvert\text{lcs}(u,v_{1\cdots i})\right\rvert,lp_i=\left\lvert\text{lcp}(v,v_{i\cdots|v|})\right\rvert$

如果存在长度为$n$的以$v_i$结尾的对称轴在$v$内的$aa$串，那么有$n\leq i\lt2n,ls_n\geq2n-i,lp_{n+1}\geq i-n$，也就是说$2n-ls_n\leq i\leq\min(2n-1,n+lp_{n+1})$，所以枚举$n$，并更新对应的$i$即可

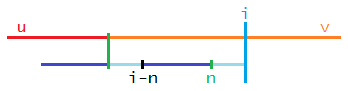
如果是求每个位置开始的最长/最短$aa$串，那么要用线段树来辅助更新，时间复杂度$O(n\log^2n)$

如果是计数，这样会重复计算那些对称轴恰好在$u,v$连接处的$aa$串，减去相应的$\sum\limits_i[ls_i=i]$即可，时间复杂度$O(n\log n)$

然后是一个查询子串border的算法，想要好复杂度的可以去看策爷ppt，这里给一个简单好写的$O(\sqrt n)$后缀数组做法

对于子串$s_{l\cdots r}$，如果要找最短的border，首先暴力找长度为$1\cdots\sqrt n$的border，如果找不到且border存在，那么这个长度$\gt\sqrt n$的border$i$（$s_{i\cdots r}=s_{l\cdots l+r-i+1}$）一定满足$i$和$l$在后缀数组中的距离$\leq\sqrt n$

证明：考虑反证，如果距离$\gt\sqrt n$，那么说明有$\gt\sqrt n$个长度$\gt\sqrt n$的不同位置的子串相等，其中一定会有重叠，也就是说我们找到了更短的border

然后是这道题，如果能在子串中找到两个相同字符，那么切割方案形如$?a?a?$，也就是说答案最多是$4$，接下来就是分类讨论了

设$lt_i$为最小的$r$使得$s_{i\cdots r}$是$aa$串，$rt_i$为最大的$l$使得$s_{l\cdots i}$是$aa$串，这两个数组可以用main and lorentz算法预处理

$-1$：没有相同字符时就无解，只有当$r-l+1\leq26$时才会发生，直接扫一遍即可

$1$：整个串形如$aa\cdots a$，如果我们找最长的$a$，那么$\frac{r-l+1}{|a|}$就是质数，所以直接枚举$r-l+1$的所有质因子即可

$2$：整个串形如$aab$或$baa$或$aba$，第一种就是$lt_l\leq r$，第二种就是$rt_r\geq l$，第三种就是问这个子串是否有长度$\leq\frac{r-l+1}2$的border

$3$：整个串形如$abac,baca,baac$，容易看出如果存在前两种方案，那么肯定有$|a|=1$，第一种就是判断$s_l$是否在$s_{l+1\cdots r}$中出现，第二种就是判断$s_r$是否在$s_{l\cdots r-1}$中出现，用前缀和即可，第三种的条件就是存在$l\leq i\leq r$使得$lt_i\leq r$，用ST表预处理得到$lt_i$的区间最小值即可

剩下的情况就是$4$了

说起来挺简单，写起来还是挺长的...

UPD:我就是个智障，这个AA串直接用[NOI2016]优秀的拆分的方法求就可以了...

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
using namespace std;
const int inf=2147483647;
char s[200010];
int n,sq;
namespace ex{
	char s[200010],t[200010];
	int nex[200010],ex[200010],n,m;
	void getnex(){
		int i,a,p;
		m=strlen(t+1);
		memset(nex,0,(m+1)<<2);
		a=p=0;
		nex[1]=m;
		for(i=2;i<=m;i++){
			if(i+nex[i-a+1]>=p){
				for(p=max(p,i);p<=m&&t[p]==t[p-i+1];p++);
				nex[i]=p-i;
				a=i;
			}else
				nex[i]=nex[i-a+1];
		}
	}
	void getex(){//ex[i]=lcp(s[i],t)
		int i,a,p;
		getnex();
		n=strlen(s+1);
		a=p=0;
		for(i=1;i<=n;i++){
			if(i+nex[i-a+1]>=p){
				for(p=max(p,i);p<=n&&p-i+1<=m&&s[p]==t[p-i+1];p++);
				ex[i]=p-i;
				a=i;
			}else
				ex[i]=nex[i-a+1];
		}
	}
}
int*po;
struct seg{
	int mn[800010];
	void build(int l,int r,int x){
		mn[x]=inf;
		if(l==r)return;
		int mid=(l+r)>>1;
		build(l,mid,x<<1);
		build(mid+1,r,x<<1|1);
	}
	void fmin(int x,int v){
		if(v<mn[x])mn[x]=v;
	}
	void pushdown(int x){
		if(mn[x]!=inf){
			fmin(x<<1,mn[x]);
			fmin(x<<1|1,mn[x]);
			mn[x]=inf;
		}
	}
	void modify(int L,int R,int v,int l=1,int r=n,int x=1){
		if(L<=l&&r<=R)return fmin(x,v);
		pushdown(x);
		int mid=(l+r)>>1;
		if(L<=mid)modify(L,R,v,l,mid,x<<1);
		if(mid<R)modify(L,R,v,mid+1,r,x<<1|1);
	}
	void dfs(int l,int r,int x){
		if(l==r){
			po[l]=mn[x];
			return;
		}
		pushdown(x);
		int mid=(l+r)>>1;
		dfs(l,mid,x<<1);
		dfs(mid+1,r,x<<1|1);
	}
}sl,sr;
namespace mainlo{
	int ls[200010],lp[200010],pos;
	void newright(char*a,int n,char*b,int m,bool f){
		memcpy(ex::t+1,b+1,m);
		ex::t[m+1]=0;
		ex::getnex();
		memcpy(lp,ex::nex,(m+1)<<2);
		lp[m+1]=0;
		reverse(a+1,a+n+1);
		reverse(b+1,b+m+1);
		memcpy(ex::s+1,b+1,m);
		ex::s[m+1]=0;
		memcpy(ex::t+1,a+1,n);
		ex::t[n+1]=0;
		ex::getex();
		memcpy(ls,ex::ex,(m+1)<<2);
		reverse(ls+1,ls+m+1);
		int i,st,en;
		for(i=1;i<=m;i++){
			st=2*i-ls[i];
			en=min(2*i-1,i+lp[i+1]);
			if(st<=en){
				if(f){
					sl.modify(pos+st-2*i+1,pos+en-2*i+1,i*2);
					sr.modify(pos+st,pos+en,i*2);
				}else{
					sl.modify(pos-en,pos-st,i*2);
					sr.modify(pos-en+i*2-1,pos-st+i*2-1,i*2);
				}
			}
		}
	}
	void solve(int l,int r){
		if(l==r)return;
		int mid=(l+r)>>1,ln=mid-l+1,rn=r-mid;
		pos=mid;
		newright(s+l-1,ln,s+mid,rn,1);
		pos=mid+1;
		newright(s+mid,rn,s+l-1,ln,0);
		solve(l,mid);
		solve(mid+1,r);
	}
}
namespace sa{
	int rk[400010],sa[200010],h[200010],c[200010],mn[200010][18],lg[200010];
	struct pr{
		int c[2],i;
		pr(int a=0,int b=0,int d=0):c{a,b},i(d){}
	}p[200010],q[200010];
	bool operator!=(pr a,pr b){return a.c[0]!=b.c[0]||a.c[1]!=b.c[1];}
	void sort(int f){
		int m,i;
		memset(c,0,sizeof(c));
		for(i=1,m=0;i<=n;i++){
			c[p[i].c[f]]++;
			m=max(m,p[i].c[f]);
		}
		for(i=1;i<=m;i++)c[i]+=c[i-1];
		for(i=n;i>0;i--)q[c[p[i].c[f]]--]=p[i];
		memcpy(p,q,sizeof(q));
	}
	void suf(){
		int i,j,l,m;
		for(i=1;i<=n;i++)rk[i]=s[i]-'a'+1;
		for(l=1;l<=n;l<<=1){
			for(i=1;i<=n;i++)p[i]=pr(rk[i],rk[i+l],i);
			sort(1);
			sort(0);
			for(i=1,m=0;i<=n;i++){
				if(p[i]!=p[i-1])m++;
				rk[p[i].i]=m;
			}
		}
		for(i=1;i<=n;i++)sa[rk[i]]=i;
		for(i=1,l=0;i<=n;i++){
			if(l)l--;
			while(s[i+l]==s[sa[rk[i]-1]+l])l++;
			h[rk[i]]=l;
		}
		for(i=1;i<=n;i++)mn[i][0]=h[i];
		for(j=1;j<18;j++){
			for(i=1;i+(1<<j)-1<=n;i++)mn[i][j]=min(mn[i][j-1],mn[i+(1<<(j-1))][j-1]);
		}
		for(i=2;i<=n;i++)lg[i]=lg[i>>1]+1;
	}
	int query(int l,int r){
		int k=lg[r-l+1];
		return min(mn[l][k],mn[r-(1<<k)+1][k]);
	}
	int lcp(int x,int y){
		if(rk[x]>rk[y])swap(x,y);
		return query(rk[x]+1,rk[y]);
	}
	int border(int l,int r){
		int i,s=inf;
		for(i=1;i<=sq&&i<r-l+1;i++){
			if(lcp(l,r-i+1)>=i)return i;
		}
		for(i=max(1,rk[l]-sq+1);i<=min(n,rk[l]+sq-1);i++){
			if(l<sa[i]&&sa[i]<=r&&lcp(l,sa[i])>=r-sa[i]+1)s=min(s,r-sa[i]+1);
		}
		return s==inf?inf/2:s;
	}
}
int lt[200010],rt[200010];
bool vis[30];
bool checkno(int l,int r){
	if(r-l+1>26)return 0;
	memset(vis,0,sizeof(vis));
	for(int i=l;i<=r;i++){
		if(vis[s[i]-'a'])return 0;
		vis[s[i]-'a']=1;
	}
	return 1;
}
vector<int>pd[200010];
bool check1(int l,int r){
	for(int&t:pd[r-l+1]){
		if(sa::lcp(l,l+(r-l+1)/t)>=r-l+1-(r-l+1)/t)return 1;
	}
	return 0;
}
bool check2(int l,int r){
	return lt[l]<=r||rt[r]>=l||sa::border(l,r)*2<=r-l+1;
}
int sum[200010][26];
int get(int l,int r,int c){
	return sum[r][c-'a']-sum[l-1][c-'a'];
}
int mn[200010][18],lg[200010];
int qmin(int l,int r){
	int k=lg[r-l+1];
	return min(mn[l][k],mn[r-(1<<k)+1][k]);
}
bool check3(int l,int r){
	return get(l+1,r,s[l])||get(l,r-1,s[r])||qmin(l,r)<=r;
}
int query(int l,int r){
	if(checkno(l,r))return-1;
	if(check1(l,r))return 1;
	if(check2(l,r))return 2;
	if(check3(l,r))return 3;
	return 4;
}
int main(){
	int m,i,j,l,r;
	scanf("%d%s",&n,s+1);
	sq=sqrt(n);
	sl.build(1,n,1);
	sr.build(1,n,1);
	mainlo::solve(1,n);
	po=lt;
	sl.dfs(1,n,1);
	po=rt;
	sr.dfs(1,n,1);
	sa::suf();
	for(i=1;i<=n;i++)lt[i]=lt[i]==inf?n+1:i+lt[i]-1;
	for(i=1;i<=n;i++)rt[i]=rt[i]==inf?0:i-rt[i]+1;
	for(i=2;i<=n;i++){
		if(pd[i].empty()){
			for(j=i;j<=n;j+=i)pd[j].push_back(i);
		}
	}
	for(i=1;i<=n;i++){
		memcpy(sum[i],sum[i-1],sizeof(sum[i-1]));
		sum[i][s[i]-'a']++;
	}
	for(i=1;i<=n;i++)mn[i][0]=lt[i];
	for(j=1;j<18;j++){
		for(i=1;i+(1<<j)-1<=n;i++)mn[i][j]=min(mn[i][j-1],mn[i+(1<<(j-1))][j-1]);
	}
	for(i=2;i<=n;i++)lg[i]=lg[i>>1]+1;
	scanf("%d",&m);
	while(m--){
		scanf("%d%d",&l,&r);
		printf("%d\n",query(l,r));
	}
}