uva 1660 & poj 1966(点连通度）

Cable TV Network

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 4267		Accepted: 2003

Description

The interconnection of the relays in a cable TV network is bi-directional. The network is connected if there is at least one interconnection path between each pair of relays present in the network. Otherwise the network is disconnected. An empty network or a network with a single relay is considered connected. The safety factor f of a network with n relays is: 
1. n, if the net remains connected regardless the number of relays removed from the net. 
2. The minimal number of relays that disconnect the network when removed. 

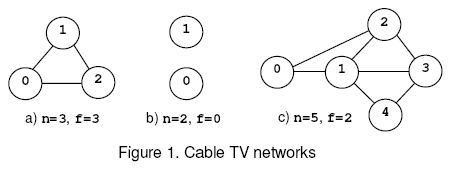
For example, consider the nets from figure 1, where the circles mark the relays and the solid lines correspond to interconnection cables. The network (a) is connected regardless the number of relays that are removed and, according to rule (1), f=n=3. The network (b) is disconnected when 0 relays are removed, hence f=0 by rule (2). The network (c) is disconnected when the relays 1 and 2 or 1 and 3 are removed. The safety factor is 2.

Input

Write a program that reads several data sets from the standard input and computes the safety factor for the cable networks encoded by the data sets. Each data set starts with two integers: 0<=n<=50,the number of relays in the net, and m, the number of cables in the net. Follow m data pairs (u,v), u < v, where u and v are relay identifiers (integers in the range 0..n-1). The pair (u,v) designates the cable that interconnects the relays u and v. The pairs may occur in any order.Except the (u,v) pairs, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.

Output

For each data set, the program prints on the standard output, from the beginning of a line, the safety factor of the encoded net.

Sample Input

0 0
1 0
3 3 (0,1) (0,2) (1,2)
2 0
5 7 (0,1) (0,2) (1,3) (1,2) (1,4) (2,3) (3,4)

Sample Output

0
1
3
0
2

Hint

The first data set encodes an empty network, the second data set corresponds to a network with a single relay, and the following three data sets encode the nets shown in figure 1.

Source

Southeastern Europe 2004

图的连通度问题是指：在图中删去部分元素（点或边），使得图中指定的两个点s和t不连通 （不存在从s到t的路径），求至少要删去几个元素。

图的连通度分为点连通度和边连通度：

（1）点连通度：只许删点，求至少要删掉几个点（当然，s和t不能删去，这里保证原图中至少有三个点）；

（2）边连通度：只许删边，求至少要删掉几条边。

并且，有向图和无向图的连通度求法不同，因此还要分开考虑（对于混合图，只需将其中所有的无向边按照 
无向图的办法处理、有向边按照有向图的办法处理即可）。

【1】有向图的边连通度： 
这个其实就是最小割问题。以s为源点，t为汇点建立网络，原图中的每条边在网络中仍存在，容量为1，求该网络的最小割（也就是最大流）的值即为原图的边连通度。 
【2】有向图的点连通度： 
需要拆点。建立一个网络，原图中的每个点i在网络中拆成i'与i''，有一条边<i', i''>，容量为1 （<s', s''>和<t', t''>例外，容量为正无穷）。原图中的每条边<i, j>在网络中为边<i'', j'>， 
容量为正无穷。以s'为源点、t''为汇点求最大流，最大流的值即为原图的点连通度。 
说明：最大流对应的是最小割。显然，容量为正无穷的边不可能通过最小割，也就是原图中的边和s、t两个点不能删去；若边<i, i''>通过最小割，则表示将原图中的点i删去。
【3】无向图的边连通度： 
将图中的每条边(i, j)拆成<i, j>和<j, i>两条边，再按照有向图的办法（【1】）处理； 
【4】无向图的点连通度： 
将图中的每条边(i, j)拆成<i, j>和<j, i>两条边，再按照有向图的办法（【2】）处理。

关键就是建图，然而我并不懂为什么这样建。。。

#include <cstdio>
#include <iostream>
#include <sstream>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <string>
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <algorithm>
using namespace std;
#define ll long long
#define _cle(m, a) memset(m, a, sizeof(m))
#define repu(i, a, b) for(int i = a; i < b; i++)
#define repd(i, a, b) for(int i = b; i >= a; i--)
#define sfi(n) scanf("%d", &n)
#define pfi(n) printf("%d\n", n)
#define sfi2(n, m) scanf("%d%d", &n, &m)
#define pfi2(n, m) printf("%d %d\n", n, m)
#define pfi3(a, b, c) printf("%d %d %d\n", a, b, c)
#define MAXN 105
#define V 55
const int INF = 0x3f3f3f3f;
int edge[V][V];
int N,M;
int n,m;
#define maxn 210
const int inf = 0x3f3f3f3f;

struct EK
{
    int cap[maxn][maxn];
    int flow[maxn][maxn];
    int n;
    void init(int n)
    {
        this->n = n;
        memset(cap, , sizeof(cap));
    }
    void addCap(int i, int j, int val)
    {
        cap[i][j] = val;
    }
    int solve(int source, int sink)
    {
        if(source == sink)    return inf;///源=汇, 流量无穷大！
        static int que[maxn], pre[maxn], d[maxn];
///bfs时的队列; bfs时某点的前驱; 增光路径的流量
        int p, q, t;///bfs时的队列底、顶; bfs时当前元素
        memset(flow, , sizeof(flow));
        while(true)
        {
            memset(pre, , sizeof(pre));
            d[source] = inf;
            p = q = ;
            que[q ++] = source;

            while(p<q && pre[sink]==-)
            {
                t = que[p ++];
                for(int i = ; i < n; i ++)  //注意下标
                {
                    if(pre[i]==- && cap[t][i]-flow[t][i]>)
                    {
///残余=cap-flow
                        pre[i] = t;
                        que[q++]=i;
                        d[i] = min(d[t], cap[t][i]-flow[t][i]);
                    }
                }
            }
            if(pre[sink]==-)    break;///没有增广路径了！
            for(int i = sink; i != source; i = pre[i])
            {
                flow[pre[i]][i] += d[sink];
                flow[i][pre[i]] -= d[sink];
            }
        }
        t = ;///当做网络流量
        for(int i = ; i < n; i ++)
            t += flow[source][i];
        return t;
    }
}ek;

char s[];
//void init()
//{
//    _cle(vis, 0);
//    _cle(pre, 0);
//    _cle(anc, 0);
//    _cle(deg, 0);
//    _cle(edge, 0);
//}
int main()
{
    int n, m;
    while(~sfi2(n, m))
    {
        //init();
        _cle(edge, );
        ek.init( * n);
        repu(i, , m)
        {
            scanf("%s", s);
            int x = , y = ;
            if(s[] == ',')
            {
                x = s[] - '';
                if(s[] == ')') y = s[] - '';
                else y = (s[] - '') *  + s[] - '';
            }
            else
            {
                x = (s[] - '') *  + s[] - '';
                if(s[] == ')') y = s[] - '';
                else y = (s[] - '') *  + s[] - '';
            }
            edge[x][y] = edge[y][x] = ;
            //pfi2(x, y);
        }

        //repu(i, 0, n) pfi2(i, deg[i]);
        repu(i, , n) ek.addCap(i, i + n, );

        repu(i, , n) repu(j, , n)
        if(edge[i][j]) ek.addCap(i + n, j, inf);

        int minn = n, ans;
        repu(i, , n) repu(j, , n)
        {
            ek.addCap(i, i + n, inf);
            ek.addCap(j, j + n, inf);
            ans = ek.solve(i, j);
            ek.addCap(i, i + n, );
            ek.addCap(j, j + n, );
            //pfi(ans);
            minn = min(ans, minn);
        }
        pfi(minn);
    }
    return ;
}