Taylor series Explicit Euler Implicit Euler

1 Taylor series

\[\begin{gathered}\sum_{n=0}^{\infty}\frac{f^{(n)}\left(a\right)}{n!}\left(x-a\right)^{n}\\f\left(a\right)+\frac{f^{\prime}\left(a\right)}{1!}(x-a)+\frac{f^{\prime\prime}\left(a\right)}{2!}(x-a)^{2}+\frac{f^{\prime\prime\prime}\left(a\right)}{3!}(x-a)^{3}+\ldots\end{gathered}
\]

\[y(t+\Delta t)=y(t)+\Delta ty'(t)+\frac{1}{2}\Delta t^{2}y''(t)+\frac{1}{3!}\Delta t^{3}y'''(t)+...
\]

2 Explicit Euler

\[\Delta{t} = t_1 - t_0
\]

\[\begin{aligned}
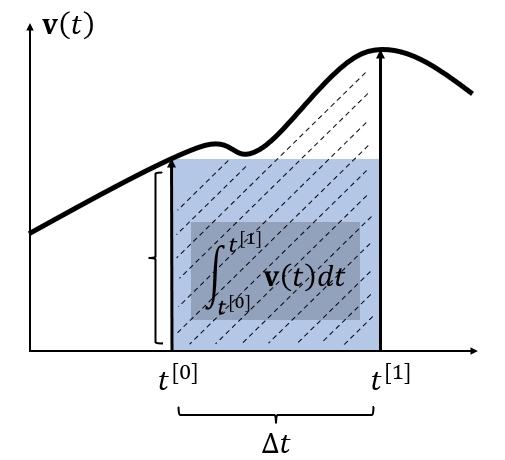
\int_{t^{[0]}}^{t^{[1]}}\mathbf{v}(t)dt& =\Delta t\mathbf{v}\big(t^{[0]}\big)+\frac{\Delta t^{2}}{2}\mathbf{v}'\big(t^{[0]}\big)+\cdots \\
&=\Delta t\left.\mathbf{v}(t^{[0]}) + O(\Delta t^2)\right.
\end{aligned}
\]

\[\mathbf{x}\big(t^{[1]}\big) - \mathbf{x}\big(t^{[0]}\big) = [\text{Taylor at } \mathbf{x}\big(t^{[1]}\big) \text{ based on } \mathbf{x}\big(t^{[0]}\big)] - \mathbf{x}\big(t^{[0]}\big)
\]

3 Implicit Euler

\[\Delta{t} = t_1 - t_0
\]

\[\begin{aligned}
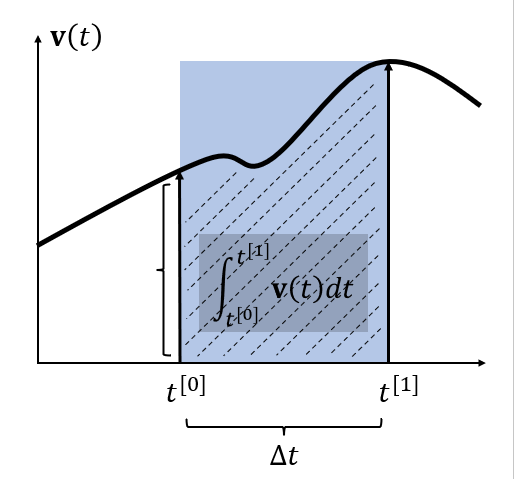
\int_{t^{[0]}}^{t^{[1]}}\mathbf{v}(t)dt& =\Delta t\mathbf{v}\big(t^{[1]}\big)-\frac{\Delta t^{2}}{2}\mathbf{v}'\big(t^{[1]}\big)+\cdots \\
&=\Delta t\left.\mathbf{v}(t^{[1]})+O(\Delta t^2)\right.
\end{aligned}
\]

\[\mathbf{x}\big(t^{[1]}\big) - \mathbf{x}\big(t^{[0]}\big) = \mathbf{x}\big(t^{[1]}\big) - [\text{Taylor at } \mathbf{x}\big(t^{[0]}\big) \text{ based on } \mathbf{x}\big(t^{[1]}\big)]
\]

X ref

1. Euler's Method, Taylor Series Method, Runge Kutta ... Brown University
2. Mathew Mariani Midpoint Integration
3. GAMES103: Intro to Physics-Based Animation by Rigid Body Dynamics