ZCMU-1144

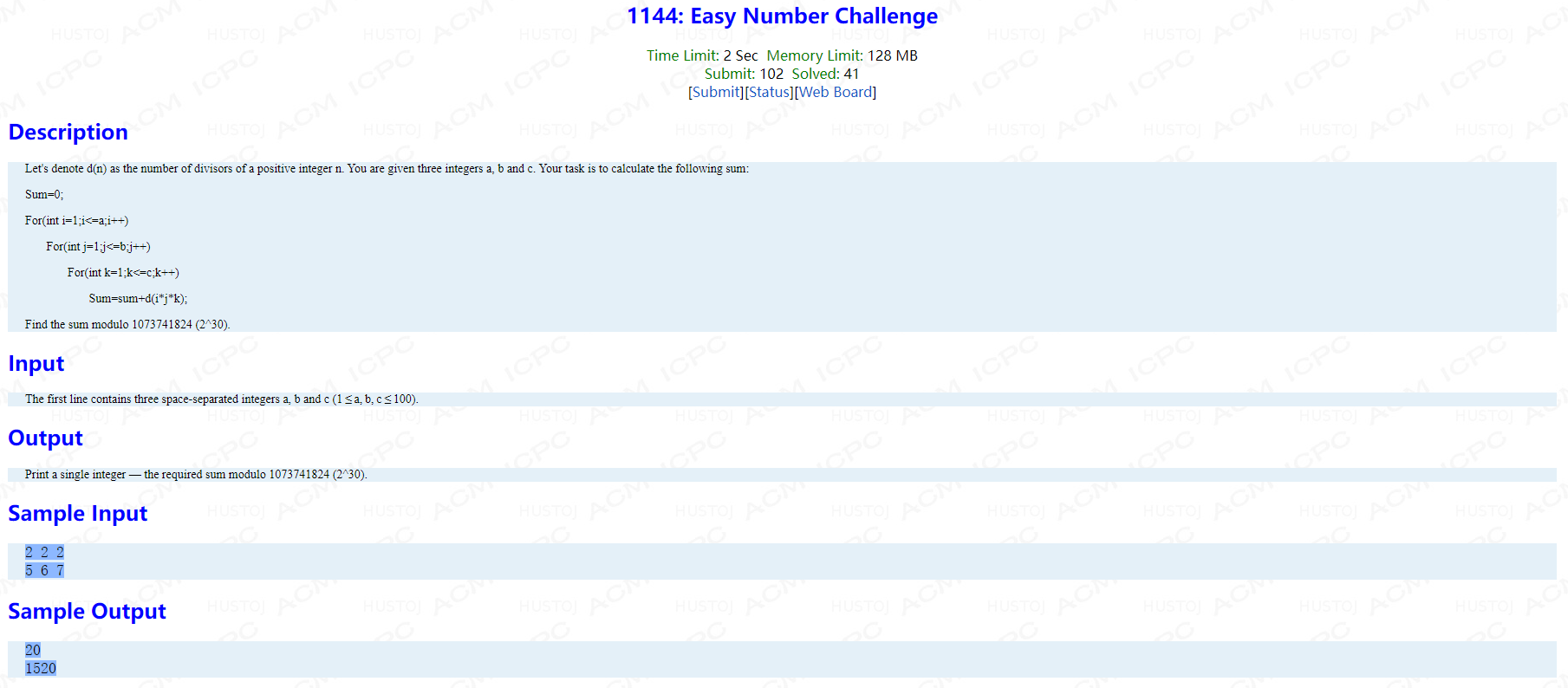
简单问题：

就只是如何降低时间的问题罢了：本来这种方法以前学过但是没怎么用所以不太灵活、

#include<stdio.h>
#define maxn 1000010
int sum[maxn]={0};
void Sum(){
	for(int i=1;i<=maxn;i++){
        for(int j=i;j<=maxn;j+=i){
            sum[j]++;
            //表示有i那样的因子
			//这样可以快速得到所要的情况
        }
    }
}
int main(){
    Sum();
    int a,b,c;
    while(~scanf("%d%d%d",&a,&b,&c)){
        int sum1=0;
        for(int i=1;i<=a;i++){
            for(int j=1;j<=b;j++){
                for(int k=1;k<=c;k++){
                    sum1=(sum1+sum[i*j*k])%1073741824;
                }
            }
        }
        printf("%d\n",sum1);
    }
    return 0;
}