闲话 717 - LGV 引理的小应用

这是我们的某一天的联考题目：

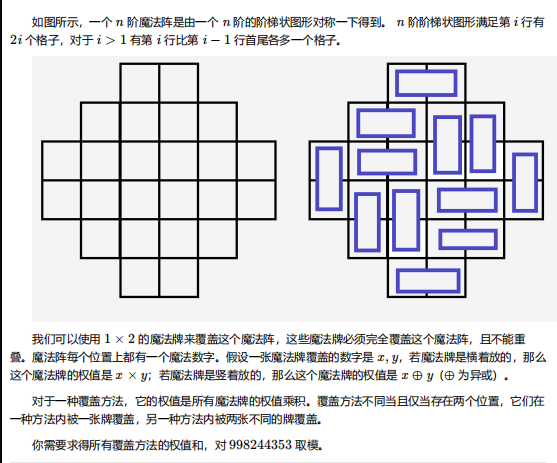
\(n\le 500\)。

显然使用平面图完美匹配计数可以获得 \(O(n^6)\)，但是有一种神秘的对路径的双射。当时我们都认为这是超级人类智慧，但是今天看书发现是书上的某个例的题的方法（有不同）。。

考虑对正六边形的菱形密铺方案数（上图）。

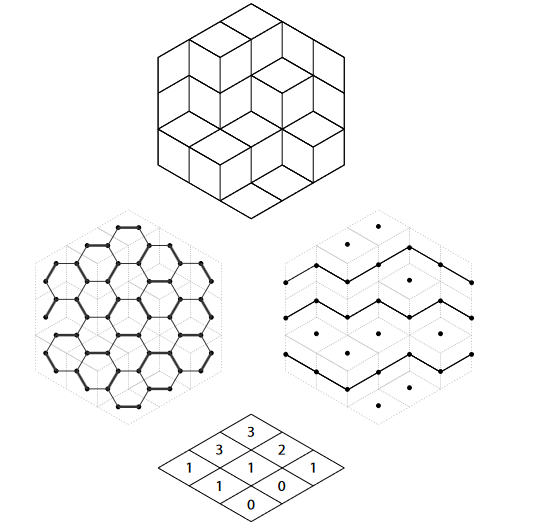
可以等价的问题是完美匹配。但是另一种听上去很扯淡但是实际正确的看法是顺从自己的眼睛把这个图看作小立方体的堆叠图。这样，我们的路径就是贴着等高的小立方体的外面的面走的路径。然后显然这是双射。

放在原图上来看，我到底干了什么事情：我指定了一种从密铺的一个骨牌一边转移到另一边的一个规则；而之所以我能只考虑按这个规则转移的路径，是因为其他不在路径上的东西我们是确定的——全都横着。我的路径也恰好全是竖着的。

注：这相当于非标准杨表计数（当时不知道这一点），不用 LGV 引理。不过反正带上权都得死。

现在以这种想法来看联考题。首先好像立体的思维不再奏效，但是仍然可以类似分析。注意到：

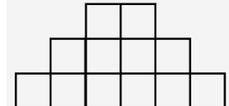
这样的图形的密铺是唯一的。因此我要构造的应该是从斜边启程（这样保证了上面和中间的东西必须横着）

此外想想我们构造的路径怎么走：然后横着的骨牌肯定只能横着穿过走，竖着的骨牌如果不横着走就只能改变上下格子。这样我们差不多就构造出了路径：

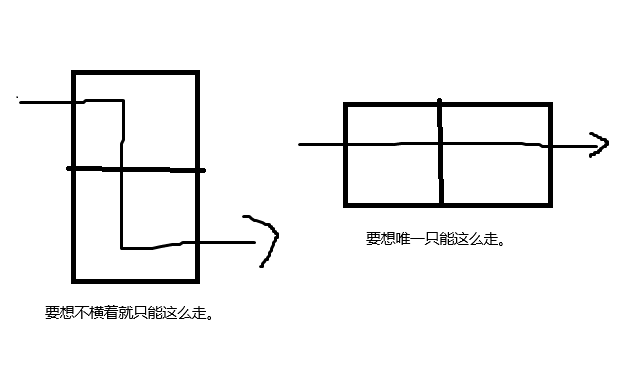
然后利用 LGV 引理计算即可。

upd：

多看了几行，这个不是接下来书上的 Schroder determinants and Aztec diamonds 吗！！搬题无疑了