Python汉罗塔

第一步代码：

import turtle

class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return len(self.items) == 0
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        if not self.isEmpty():
            return self.items[len(self.items) - 1]
    def size(self):
        return len(self.items)

def drawpole_3():#画出汉诺塔的poles
    t = turtle.Turtle()
    t.hideturtle()
    def drawpole_1(k):
        t.up()
        t.pensize(10)
        t.speed(100)
        t.goto(400*(k-1), 100)
        t.down()
        t.goto(400*(k-1), -100)
        t.goto(400*(k-1)-20, -100)
        t.goto(400*(k-1)+20, -100)
    drawpole_1(0)#画出汉诺塔的poles[0]
    drawpole_1(1)#画出汉诺塔的poles[1]
    drawpole_1(2)#画出汉诺塔的poles[2]

def creat_plates(n):#制造n个盘子
    plates=[turtle.Turtle() for i in range(n)]
    for i in range(n):
        plates[i].up()
        plates[i].hideturtle()
        plates[i].shape("square")
        plates[i].shapesize(1,8-i)
        plates[i].goto(-400,-90+20*i)
        plates[i].showturtle()
    return plates

def pole_stack():#制造poles的栈
    poles=[Stack() for i in range(3)]
    return poles

def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
    mov=poles[fp].peek()
    plates[mov].goto((fp-1)*400,150)
    plates[mov].goto((tp-1)*400,150)
    l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
    plates[mov].goto((tp-1)*400,-90+20*l)

def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
    if height >= 1:
        moveTower(plates,poles,height-1,fromPole,withPole,toPole)
        moveDisk(plates,poles,fromPole,toPole)
        poles[toPole].push(poles[fromPole].pop())
        moveTower(plates,poles,height-1,withPole,toPole,fromPole)

myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
    poles[0].push(i)
moveTower(plates,poles,n,0,2,1)
myscreen.exitonclick()
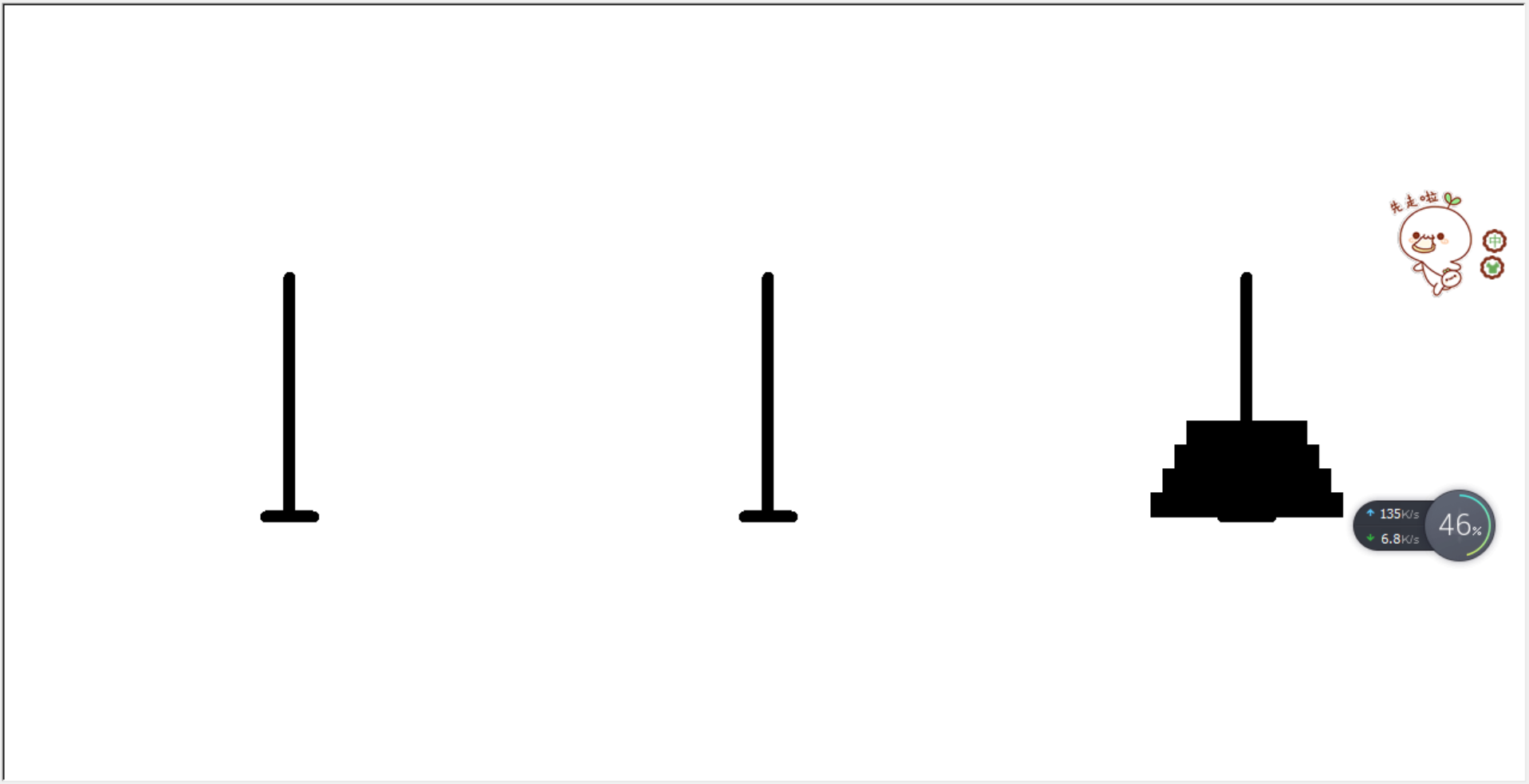
第二步用turtle画（无法截动图）汉罗塔4层如下：