基于C#程序设计语言的三种组合算法

基于C#程序设计语言的三种组合算法

1. 总体思路

1.1 前言

最近有个项目要求对多种材料进行装箱，我需要给出装箱的可能，这些材料进行过分组，每组中大致选取2-3个材料进行装箱。由于无法得知箱子大小（无法对组合数的m进行限制），材料会扩充，随之分组也会扩充（无法对组合数的n进行限制），所以理论上说能产生的组合是无限的，这当然无法实现，但我们还是能通过用户的输入来进行最大可能的处理。

1.2 算法思路

组合算法思路是比较简单的（以下所有数据都可以想象成string[]类型的），获取源数据S,C(1,n)的结果S1，将S的每个元素与S1进行相应组合得到C(2,n)的结果S2(思路演示见图1.2.1)，S2，将S的每个元素与S2进行相应组合，得到S3...重复这个过程得到Sn。

S的元素与Si进行组合的方式不同获得的组合结果不同，如果和元素本身进行了组合，组合结果就包括了与自身组合。

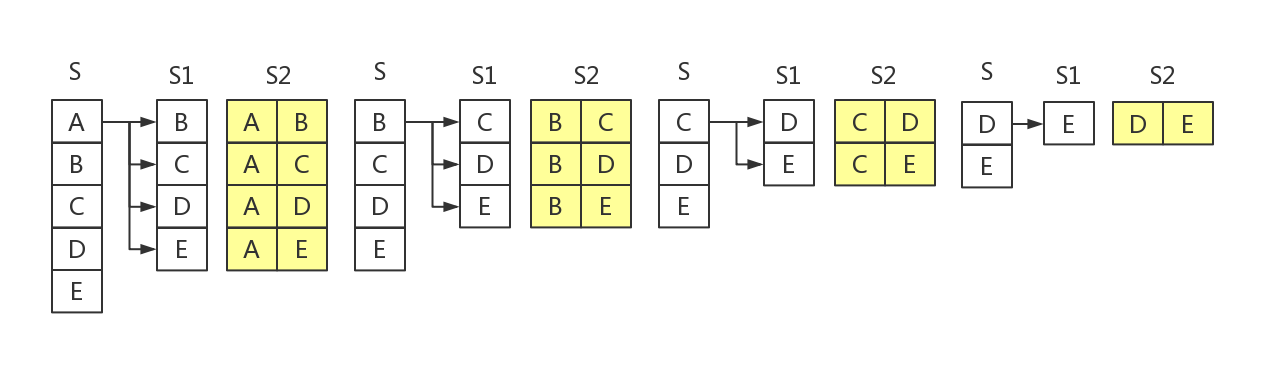
图1.1 C(2, n)组合过程

1.3 算法需要注意的点

虽然思路比较简单，但是处理起来还是有些地方需要注意。在每次进行组合时，需要对Si进行去头处理。

去头处理：去掉Si中不能与S[i]组合的元素

在不同的组合中去掉的头也不同。在与S1组合时，每次去掉的只有一组元素[A],[B],[C],[D],[E]，但在与S2组合时，去掉的头分别是：[A,B],[A,C],[A,D],[A,E]（4组），[B,C],[B,D],[B,E]（3组），[C,D],[C,E]（2组），[D,E]（1组）。推过推演可以发现，这组数据是有规律的，根据1.2，1.3小节总结出来的规律，大致可以构建出组合算法了。

2. 三种组合算法

2.1 普通组合算法

在第1章已经介绍了普通组合算法的思路，这里主要说明如何用C#代码来处理组合运算，首先需要定义三个List<string>类型src，res，tmp，src用来存储需要进行组合处理的源数据，res用来存储组合处理后的数据，tmp用来存储在操作过程中的临时数据。定义一个int[] rm变量用来存储每次需要去头的个数（例如src=[A,B,C,D,E]，进行第一次组合时，rm = [1,1,1,1], 进行第二次组合时，rm = [4,3,2,1]）。

string[] Combination(List<string> src, List<string> res, List<string> tmp, ref int[] rm, int rsp, int tmp_index, int rp)

{

	if(res.Count() == 0)

    {

    	return tmp;

    }

	if(rsp == res.Count())

    {

    	src.Removerange(0, 1);

        res.Removerange(0, rm[rp]);

        rm[rp] = rsp;

        rsp = 0;

        rp += 1;

    }

	tmp[tmp_index] = src[0] + "," + res[rsp];

    tmp = Combination(src, res, tmp, rm, rsp + 1, tmp_index + 1, rp);

    return tmp;

}

代码清单2.1 普通组合算法

2.2 与自身进行组合的组合算法

本节思路及代码与2.1小节大同小异，故先略过。

2.3 组合元素进行过分组限制的组合算法

现在要求将元素进行分组，每组的元素个数随机，从每组最多选择x个元素进行组合。这种算法只需要在普通组合算法程序中进行一些条件限制便可以实现，最主要需要注意的问题是，rm中存储的数据不同了（对下次去掉的头有了限制）。由于rm[rp]不再是rsp了，所以需要新的变量count来计算下次需要去掉的头。

string[] Combination(List<string> src, List<string> res, List<string> tmp, ref int[] rm, int rsp, int tmp_index, int rp， int count)

{

	if(res.Count() == 0)

    {

    	return tmp;

    }

	if(rsp == res.Count())

    {

    	src.Removerange(0, 1);

        res.Removerange(0, rm[rp]);

        rm[rp] = count;

        rsp = 0;

        rp += 1;

    }

    //	...

    //	检测是否属于同一分组，如果属于同一分组，则bool bl = true；

    //	...

    if(bl == true)

    	tmp = Combination(src, res, tmp, rm, rsp + 1, tmp_index + 1, rp);

    else

    {

    	tmp[tmp_index] = src[0] + "," + res[rsp];

        count++;

    }

    return tmp;

}

代码清单2.2 有分组限制的组合算法

代码清单2.2中，省略了“检测是否属于同一分组”的代码，因为不同需求的初始条件不一样，故略过了此段代码。在我涉及到的需求中，我是将分组内容用DataTable存储，然后“检测同一分组”时会去表中检索，以此来判断是否属于同一分组。对于检测，我将所需要检测的内容组合成一个数组，然后检测首元素是否与指向元素属于同一分组，如果属于，bool bl为true，如果不属于，则为false。

我将所需要检测的内容组合成一个数组，然后定义两个指针（索引）pa，pb，pa与pb初始都指向首元素，若pa内容与pb内容相等，则count++，若pa内容与pb内容不等，则pa = pb + 1，再重复上述步骤，这样可以统计出一个组内包含多少个成员。

3. 请使用循环替代递归

最后，请使用循环来带起递归过程，因为递归未结束时，是不会释放内存的，在数据量大时，会造成内存溢出的错误，所以，请使用循环。

PS: 本文所涉及的代码均未经过编译，若出现错误请进行修改。