fisher 判决方式是监督学习，在新样本加入之前，已经有了原样本。

原样本是训练集，训练的目的是要分类，也就是要找到分类线。一刀砍成两半！

当样本集确定的时候，分类的关键就在于如何砍下这一刀！

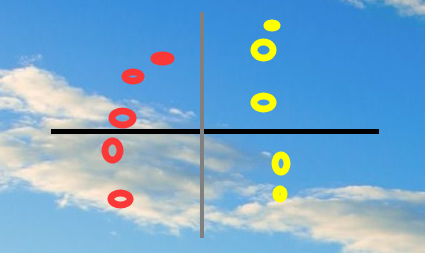
若以黑色的来划分，很明显不合理，以灰色的来划分，才是看上去合理的

1.先确定砍的方向

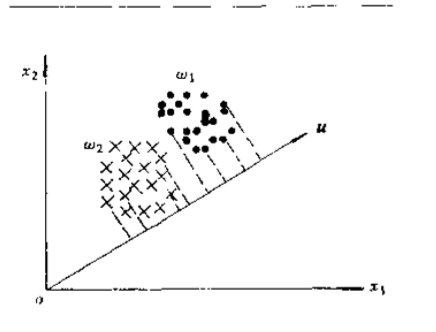
关键在于如何找到投影的向量u，与u的长度无关。只看方向

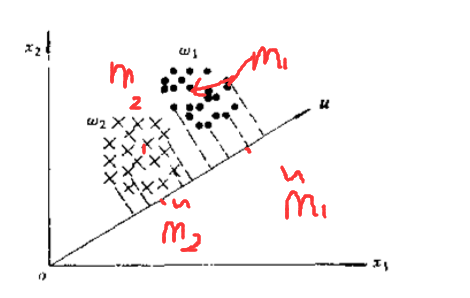
找到样本点的中心均值m1，m2，以及在向量u上的投影的m1~，m2~。

因为u的方向与样本点都有关，所以需要考虑一个含有所有样本点的表达式

不妨算出离差阵

算出类内离差矩阵，两个都要求出来，并求和

并且投影的离差阵

根据聚类的理想情况，类内距离小，类间距离大，所以就用类间去处理类内，我们现在的变量是向量u，我们就对u求导，算出max存在的时后u的条件。

为了方便化简，引入一个参数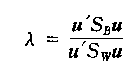 不要以为下面除以是向量，（1*2）*（2*2）（2*1）=1  维度变成1，这是一个常数。

当求导公式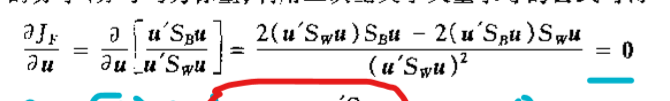

分子为0的时候，推出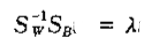

所以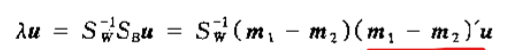

而且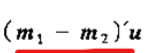是（1*2）*（2*1）等于1，也是一个常数

到此为止，u的方向已经确定了

2.具体切哪一个点。

a，切

切投影均值的终点

2.

切贝叶斯概率的比例点

方向和具体点均已找到，分析完毕

fisher线性判别的更多相关文章

  1. PRML读书会第四章 Linear Models for Classification(贝叶斯marginalization、Fisher线性判别、感知机、概率生成和判别模型、逻辑回归)

    主讲人 planktonli planktonli(1027753147) 19:52:28 现在我们就开始讲第四章,第四章的内容是关于 线性分类模型,主要内容有四点:1) Fisher准则的分类,以 ...

  2. 【线性判别】Fisher线性判别（转）

    今天读paper遇到了Fisher线性判别的变体, 所以来学习一下, 所以到时候一定要把PRMl刷一遍呀 以下两篇论文一起阅读比较好: 论文1: https://blog.csdn.net/Rainb ...

  3. 线性判别函数-Fisher 线性判别

    这是我在上模式识别课程时的内容,也有参考这里. 线性判别函数的基本概念 判别函数为线性的情况的一般表达式 式中x是d 维特征向量,又称样本向量, 称为权向量, 分别表示为 是个常数,称为阈值权. 设样 ...

  4. Fisher 线性判别

    Multiplying both sides of this result by wT and adding w0, and making use of y(x)=wTx+w0 and  y(xΓ)= ...

  5. Fisher线性判别分析

    Fisher线性判别分析 1.概述 在使用统计方法处理模式识别问题时,往往是在低维空间展开研究,然而实际中数据往往是高维的,基于统计的方法往往很难求解,因此降维成了解决问题的突破口. 假设数据存在于d ...

  6. 机器学习降维方法概括， LASSO参数缩减、主成分分析PCA、小波分析、线性判别LDA、拉普拉斯映射、深度学习SparseAutoEncoder、矩阵奇异值分解SVD、LLE局部线性嵌入、Isomap等距映射

    机器学习降维方法概括   版权声明:本文为博主原创文章,未经博主允许不得转载. https://blog.csdn.net/u014772862/article/details/52335970 最近 ...

  7. LDA（线性判别分类器）学习笔记

    Linear Discriminant Analysis(线性判别分类器)是对费舍尔的线性鉴别方法(FLD)的归纳,属于监督学习的方法. LDA的基本思想是将高维的模式样本投影到最佳鉴别矢量空间,以达 ...

  8. LDA-作为线性判别 降维 推导

    LDA 降维原理 前面对 LDA 作为作为分类器 有详细推导, 其核心就是 贝叶斯公式, 已知全概率, 求(条件概率)最大先验概率, 类似的问题. 而 LDA 如果作为 降维 的原理是: a. 将带上 ...

  9. 【模式识别与机器学习】——3.5Fisher线性判别

    ---恢复内容开始--- 出发点 应用统计方法解决模式识别问题时,一再碰到的问题之一就是维数问题. 在低维空间里解析上或计算上行得通的方法,在高维空间里往往行不通. 因此,降低维数有时就会成为处理实际 ...

随机推荐

  1. javascript基础修炼(9)——MVVM中双向数据绑定的基本原理

    开发者的javascript造诣取决于对[动态]和[异步]这两个词的理解水平. 一. 概述 1.1 MVVM模型 MVVM模型是前端单页面应用中非常重要的模型之一,也是Single Page Appl ...

  2. 【微服务目录】.NET Core 微服务介绍

    介绍: 写这篇文章有多方面的原因,第一当然是为了以后自己可以随时翻阅,第二也算是一种积累吧.因为有些东西你弄个之后,过了很长时间不用,可能会有些忘却,但是你因为以前弄个吧,有不是那种小白,需要去找示例 ...

  3. Java开发笔记（五十七）因抽象方法而产生的抽象类

    前面介绍了类的常见用法,令人感叹面向对象的强大,几乎日常生活中的所有事物,都可以抽象成Java的基类及其子类.然而抽象操作也有副作用,就是某个抽象而来的行为可能是不确定的,比如半夜鸡叫,如果是公鸡则必 ...

  4. 零基础学Python--------第8章 模块

    第8章 模块 8.1 模块概述 模块的英文是Modules,可以认为是一盒(箱)主题积木,通过它可以拼出某一个主题的东西.这与第6章介绍的函数不同,一个函数相当于一块积木,而一个模块中可以包括很多函数 ...

  5. Flask 系列之 优化项目结构

    说明 操作系统:Windows 10 Python 版本:3.7x 虚拟环境管理器:virtualenv 代码编辑器:VS Code 实验目标 完善环境配置,添加 异常请求 处理 实现 400.404 ...

  6. JS判断类型

    JS中的typeof方法可以查看数据的类型,如下: console.log(typeof 2); // number console.log(typeof "2"); // str ...

  7. Linux tail 命令

    tail 命令可用于查看文件的内容,有一个常用的参数 -f 常用于查阅正在改变的日志文件. tail -f filename 会把 filename 文件里的最尾部的内容显示在屏幕上,并且不断刷新,只 ...

  8. vmware 开启VM的硬件cpu虚拟化功能

    物理机的cpu硬件虚拟化功能,通过开启bios中的设置,而vmware中创建的虚拟机也可以开启该特性,如下. 这样的话,就直接可以基于这些VM安装openstack计算节点.控制节点.网络节点了.

  9. AS使用自带虚拟机报错解决

    Android studio自带的Google虚拟机越来越好用了,所以可以打开这个功能,想用的时候打开使用即可 使用的过程中经常会遇到这样的问题: 19:26 Emulator: emulator: ...

  10. PJProject（2.6） 工程介绍

    pjlib pjlib\build\pjlib.vcproj pjlib_test pjlib\build\pjlib_test.vcproj pjsip_core pjsip\build\pjsip ...