luoguP4705 玩游戏

好好玩

即对于k∈[1,t] 求(ax+by)^k

以下图片均来自于：

在Ta的博客查看

一

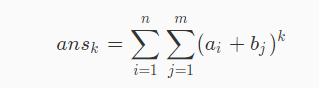
二项式展开：

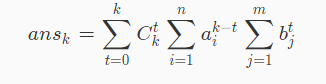
设：

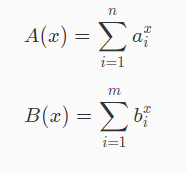
那么：

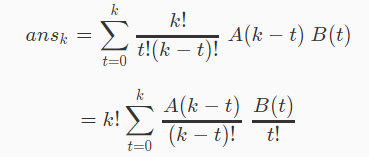
可以卷积了

二

求：

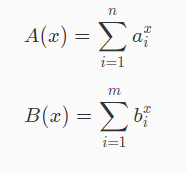
（PS：随机序列的0~k次方和，这是一个经典问题。）

我的思路：O(nk)暴力

神仙思路：求一个毫不沾边的东西，然后写两次，对应上系数。O(nlog^2n)

不妨考虑求A(x)：

先求一个看起来毫不沾边的东西：

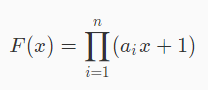
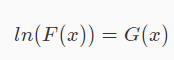
这个G成为了写两次的东西

解决问题的中轴和杠杆

利用

分治NTT+求Ln

现在已经写了一次

写第二次：

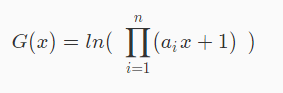
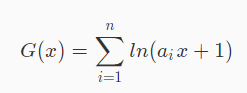
对于单独一项，采用Taylor展开，往多项式方向靠近

合起来：

交换顺序：

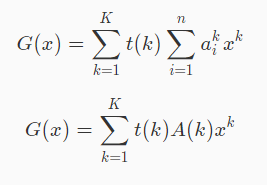
哇！

写第二次，

用Taylor展开+交换求和号

对应系数直接相等

神仙神仙~！~~~！！~！

Code

多项式全家桶

const int N=1e5+;
int n,m,K;
int a[N],b[N];
int A[N],B[N];
int c[N];
int jie[N],inv[N];
il Poly divi(int l,int r){
    if(l==r){
        Poly g;g.resize();g[]=;g[]=c[l];return g;
    }
    int mid=(l+r)>>;
    Poly L=divi(l,mid),R=divi(mid+,r);
    return L*R;
}
void wrk(int *a,int *A,int n){
    for(reg i=;i<=n;++i) c[i]=a[i];
    Poly G=divi(,n);
    // G.out();
    G.resize(K+);
    G=Ln(G);
    G.resize(K+);
    // G.out();
    for(reg k=;k<=K;++k){
        if((k+)&){
            A[k]=mod-mul(G[k],k);
        }else{
            A[k]=mul(G[k],k);
        }
    }
}
int main(){
    rd(n);rd(m);
    for(reg i=;i<=n;++i){
        rd(a[i]);
    }
    for(reg i=;i<=m;++i){
        rd(b[i]);
    }
    rd(K);
    wrk(a,A,n);
    wrk(b,B,m);
    A[]=n;
    B[]=m;
    // prt(A,0,K);
    // prt(B,0,K);

    Poly f,g;
    f.resize(K+);g.resize(K+);
    jie[]=;
    for(reg i=;i<=K;++i) jie[i]=(ll)jie[i-]*i%mod;
    inv[K]=qm(jie[K],mod-);
    for(reg i=K-;i>=;--i) inv[i]=mul(inv[i+],i+);

    for(reg i=;i<=K;++i){
        f[i]=mul(A[i],inv[i]);
        g[i]=mul(B[i],inv[i]);
    }
    f=f*g;
    for(reg i=;i<=K;++i){
        ll ans=mul(jie[i],f[i]);
        ans=mul(ans,qm(mul(n,m),mod-));
        printf("%lld\n",ans);
    }
    return ;
}