UVA 12165 Triangle Hazard

https://cn.vjudge.net/problem/UVA-12165

题目

给出D、E、F分BC，CA，AB的比$m_1:m_2$，$m_3:m_4$，$m_5:m_6$和PQR三点的坐标，求ABC三点的坐标

题解

利用梅涅劳斯定理，找出直线和三边的交点，然后每个边按顺序乘下去

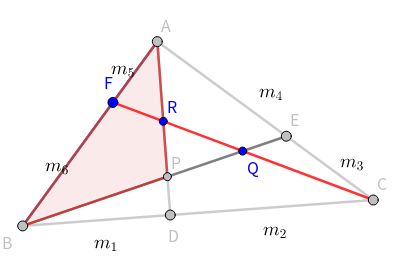
可以写出三个方程

\[\frac{AR}{RP}\cdot\boxed{\frac{PQ}{QB}}\cdot\frac{BF}{FA}=1\]

\[\frac{BP}{PQ}\cdot\boxed{\frac{QR}{RC}}\cdot\frac{CD}{DB}=1\]

\[\frac{CQ}{QR}\cdot\boxed{\frac{RP}{PA}}\cdot\frac{AE}{EC}=1\]

然后得到

\[\frac{AR}{RP}\cdot\frac{PQ}{PQ+BP}=\frac{m5}{m6}=k_1\]

\[\frac{BP}{PQ}\cdot\frac{QR}{QR+RC}=\frac{m1}{m2}=k_2\]

\[\frac{CQ}{QR}\cdot\frac{RP}{RP+RA}=\frac{m3}{m4}=k_3\]

最后解

\[x_1=k_1(1+x_2)\]

\[x_2=k_2(1+x_3)\]

\[x_3=k_3(1+x_4)\]

然后点加向量就可以得出三点坐标

AC代码

#include<cstdio>
#include<cctype>
#include<cmath>
#define REP(r,x,y) for(register int r=(x); r<(y);r++)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...) (void)0
#endif
using namespace std;

int _s; char _c;
template <class T>
inline void read(T&x) {
	x=0;
	do _c=getchar(); while(!isdigit(_c) && _c!='-');
	_s=1;
	if(_c=='-') _s=-1, _c=getchar();
	while(isdigit(_c)) { x=x*10+_c-'0'; _c=getchar();} x*=_s;
}
template<class T, class...A> inline void read(T &x, A&...a){read(x); read(a...);}

#define D point
#define CD const D
struct point {
	double x,y;
	void read() {scanf("%lf%lf",&x,&y);}
	void prn() {printf("%.8lf %.8lf",x,y);}
	};
	D operator+(CD&l, CD&r) {return (D){l.x+r.x,l.y+r.y};}
	D operator-(CD&l, CD&r) {return (D){l.x-r.x,l.y-r.y};}
	D operator/(CD&l,double a) {return (D){l.x/a,l.y/a};}
	D operator*(CD&l,double a) {return (D){l.x*a,l.y*a};}
	D operator*(double a, CD &l) {return (D){l.x*a,l.y*a};}
	double cross(CD&l, CD&r) {return l.x*r.y-l.y*r.x;}
	D intersec(CD&a, D b, CD&c, D d) {
		b=b-a; d=d-c; D u=a-c;
		double t = cross(d, u) / cross(b,d);
		return a+b*t;
	}
#undef CD
#undef D
point P,Q,R,A,B,C;
#define x1 nvdsaokvl
#define x2 nvkjdavnf
#define x3 vmasdvddz
int m1,m2,m3,m4,m5,m6;
double k1,k2,k3,x1,x2,x3;
int main() {
	int N; read(N);
	while(0<N--) {
		P.read(); Q.read(); R.read();
		read(m1,m2,m3,m4,m5,m6);
		k1=(double)m5/m6, k2=(double)m1/m2, k3=(double)m3/m4;
		double t=1-k1*k2*k3;
		x1=(k1+k1*k2*k3+k1*k2)/t;
		x2=(k2+k1*k2*k3+k2*k3)/t;
		x3=(k3+k1*k2*k3+k1*k3)/t;
		DBG("%lf %lf %lf\n", x1,x2,x3);
		A=x1*(R-P)+R;
		B=x2*(P-Q)+P;
		C=x3*(Q-R)+Q;
		A.prn();putchar(' ');
		B.prn();putchar(' ');
		C.prn();putchar('\n');
	}
	return 0;
}