[NOIP2016]换教室 题解（奇怪的三种状态）

2558. [NOIP2016]换教室

【题目描述】

对于刚上大学的牛牛来说，他面临的第一个问题是如何根据实际情况申请合适的课程。

在可以选择的课程中，有2n节课程安排在n个时间段上。在第i(1<i<n)个时间段上，两节内容相同的课程同时在不同的地点进行，其中，牛牛预先被安排在教室ci上课，而另一节课程在教室di进行。

在不提交任何申请的情况下，学生们需要按时间段的顺序依次完成所有的n节安排好的课程。如果学生想更换第i节课程的教室，则需要提出申请。若申请通过，学生就可以在第i个时间段去教室di上课，否则仍然在教室ci上课。

由于更换教室的需求太多，申请不一定能获得通过。通过计算，牛牛发现申请更换第i节课程的教室时，申请被通过的概率是一个己知的实数ki，并且对于不同课程的申请，被通过的概率是互相独立的。

学校规定，所有的申请只能在学期开始前一次性提交，并且每个人只能选择至多m节课程进行申请。这意味着牛牛必须一次性决定是否申请更换每节课的教室，而不能根据某些课程的申请结果来决定其他课程是否申请;牛牛可以申请自己最希望更换教室的m门课程，也可以不用完这m个申请的机会，甚至可以一门课程都不申请。

因为不同的课程可能会被安排在不同的教室进行，所以牛牛需要利用课间时间从一间教室赶到另一间教室。

牛牛所在的大学有v个教室，有e条道路。每条道路连接两间教室，并且是可以双向通行的。由于道路的长度和拥堵程度不同，通过不同的道路耗费的体力可能会有所不同。当第i(1<=i<=n-1)节课结束后，牛牛就会从这节课的教室出发，选择一条耗费体力最少的路径前往下一节课的教室。

现在牛牛想知道，申请哪几门课程可以使他因在教室间移动耗费的体力值的总和的期望值最小，请你帮他求出这个最小值。

【输入格式】

从文件中读入数据。

第一行四个整数n, m, v, e . n表示这个学期内的时间段的数量;m表示牛牛最多可以申请更换多少节课程的教室;v表示牛牛学校里教室的数量;e表示牛牛的学校里道路的数量。

第二行n个正整数，第i(1<=i<=n)个正整数表示ci，即第i个时间段牛牛被安排上课的教室;保证1<=ci<=v.

第三行n个正整数，第i(1<=i<=n)个正整数表示di，即第i个时间段另一间上同样课程的教室;保证1=<di<=v .

第四行n个实数，第i(1<=i<=n)个实数表示ki，即牛牛申请在第i个时间段更换教室获得通过的概率。保证0<=ki<=1。

接下来e行，每行三个正整数aj,bj,wj，表示有一条双向道路连接教室aj,bj，通过这条道路需要耗费的体力值是Wj;保证1<=aj,bj<=v,  1<=wj<=1000

保证1<=n<=2000，0<=m<=2000，1<=v<=300，0<=e<=90000。

保证通过学校里的道路，从任何一间教室出发，都能到达其他所有的教室。

保证输入的实数最多包含3位小数。

【输出格式】

输出到文件中。

输出一行，包含一个实数，四舍五入精确到小数点后恰好2位，表示答案。你的输出必须和标准输出完全一样才算正确。

测试数据保证四舍五入后的答案和准确答案的差的绝对值不大于4*10^-3(如果你不知道什么是浮点误差，这段话可以理解为:对于大多数的算法，你可以正常地使用浮点数类型而不用对它进行特殊的处理)

【样例1输入】

3 2 3 3
2 1 2
1 2 1
0.8 0.2 0.5
1 2 5
1 3 3
2 3 1

【样例1输出】

2.80

【提示】

所有可行的申请方案和期望收益如下表

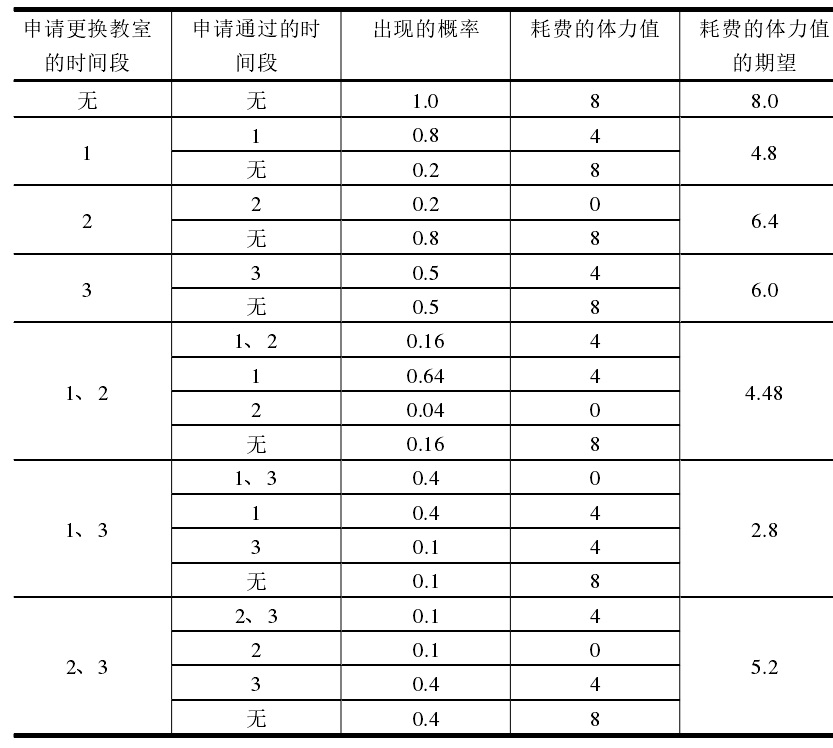
【来源】

1.道路中可能会有多条双向道路连接相同的两间教室。也有可能有道路两端连接的是同一间教室。

2.请注意区分n, m, v, e的意义，n不是教室的数量，m不是道路的数量。

　　这道题当时以为又是一个大坑，先放着没做。最近填坑时搞掉了，发现真容易。

　　不知道为啥，很多人都写两种状态，就我写了三种状态，（其实本质一样）于是调一个小坑调了半天。

　　首先基本是所有人都会去想的，状态为当前是第几节课，用了几次，现在在哪，然而这样并不可行。这道题本质是让我们去求在哪节课去申请调换，因此是否申请必须从状态之中表现出来，因此我们的状态为当前是第几节课，用了几次，这次是否申请，当时我为了方便容易自己理解，设定了三种状态，0.未申请 1.申请但失败 2.申请且成功（2,3中不体现本次是否成功的概率，仅在转移是体现）。于是这样我们的转移方程就出来了。

　　

 　　　　　　　f[i][][]=f[i-][][]+dis[c[i-]][c[i]]；
 　　　　　　　if(j<=i-) f[i][j][]=min(f[i-][j][]+dis[c1][cc],(f[i-][j][]+dis[c1][cc])*(-k[i-])+(f[i-][j][]+dis[d1][cc])*k[i-]);
             else if(j<=i-) f[i][j][]=(f[i-][j][]+dis[c1][cc])*(-k[i-])+(f[i-][j][]+dis[d1][cc])*k[i-];
             if(j==i)f[i][j][]=0x7ffffff;
             f[i][j][]=min(f[i-][j-][]+dis[c1][cc],(f[i-][j-][]+dis[c1][cc])*(-k[i-])+(f[i-][j-][]+dis[d1][cc])*k[i-]);
             f[i][j][]=min(f[i-][j-][]+dis[c1][dd],(f[i-][j-][]+dis[c1][dd])*(-k[i-])+(f[i-][j-][]+dis[d1][dd])*k[i-]);
             if(j==)
             {
                 f[i][j][]=f[i-][j-][]+dis[c1][cc];
                 f[i][j][]=f[i-][j-][]+dis[c1][dd];
             }

　　但是这样我们还有三个点是过不了的，因为我们在这里忽略了一个事情，1,2必须从同一位置转移，也就是说我们这样可能导致1,2一个是从上次申请转移过来，一个是从上次未申请转移过来，然后就WA成狗了。
　　所以我们要引进一个2.0版。
　

 　　　　　　　f[i][][]=f[i-][][]+dis[c[i-]][c[i]];
 　　　　　　　if((f[i-][j-][]+dis[c1][cc])*(1.0-k[i])+(f[i-][j-][]+dis[c1][dd])*k[i]-0.000000001>((f[i-][j-][]+dis[c1][dd])*(1.0-k[i-])+(f[i-][j-][]+dis[d1][dd])*k[i-])*k[i]+((f[i-][j-][]+dis[c1][cc])*(1.0-k[i-])+(f[i-][j-][]+dis[d1][cc])*k[i-])*(1.0-k[i]))
             {
                 f[i][j][]=(f[i-][j-][]+dis[c1][cc])*(1.0-k[i-])+(f[i-][j-][]+dis[d1][cc])*k[i-];
                 f[i][j][]=(f[i-][j-][]+dis[c1][dd])*(1.0-k[i-])+(f[i-][j-][]+dis[d1][dd])*k[i-];
             }
             else
             {
                 f[i][j][]=f[i-][j-][]+dis[c1][cc];
                 f[i][j][]=f[i-][j-][]+dis[c1][dd];

　　这样就OK了。在此感谢Q某犇提供的标程帮助我调试。

　PS:听说EZ那边的SD_le大佬联赛是也是这么打的，也是88分，欣慰～～（我这样是不是不太好）。

 #include<iostream>
 #include<cstdlib>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<map>
 #include<queue>
 #include<string>
 #include<cmath>
 using namespace std;
 int n,m,v,e,zz;
 int c[],a[],d[];
 double k[];
 struct ro{
     int to;
     double l;
     int next;
 }road[];
 void build(int x,int y,int z){
     zz++;
     road[zz].to=y;
     road[zz].next=a[x];
     road[zz].l=z;
     a[x]=zz;
 }
 bool rd[];
 double dis[][];
 queue<int> q1;
 void spfa(int t){
     memset(rd,,sizeof(rd));
     rd[t]=;
     dis[t][t]=0.0;
     q1.push(t);
     while(!q1.empty())
     {
         int x=q1.front();
         q1.pop();
         rd[x]=;
         for(int i=a[x];i>;i=road[i].next)
         {
             int y=road[i].to;
             if(dis[t][y]>dis[t][x]+road[i].l)
             {
                 dis[t][y]=dis[t][x]+road[i].l;
                 if(!rd[y])
                 {
                     rd[y]=;
                     q1.push(y);
                 }
             }
         }
     }
 }
 double f[][][];
 int main(){
     freopen("classrooma.in","r",stdin);
     freopen("classrooma.out","w",stdout);
     scanf("%d%d%d%d",&n,&m,&v,&e);
     for(int i=;i<=v;i++)
         for(int j=;j<=v;j++)
             dis[i][j]=0x7fffffff;
     for(int i=;i<=n;i++)
         scanf("%d",&c[i]);
     for(int i=;i<=n;i++)
         scanf("%d",&d[i]);
     for(int i=;i<=n;i++)
         scanf("%lf",&k[i]);
     for(int i=;i<=e;i++)
     {
         int x,y,z;
         scanf("%d%d%d",&x,&y,&z);
         build(x,y,z);
         build(y,x,z);
     }
     for(int i=;i<=v;i++)
     {
         dis[][i]=dis[i][]=0.0;
         spfa(i);
     }
     k[]=;
     f[][][]=f[][][]=0.0;
     for(int i=;i<=n;i++)
     {
         f[i][][]=f[i-][][]+dis[c[i-]][c[i]];
         for(int j=;j<=m;j++)
         {
             if(j>i)break;
             int cc=c[i],c1=c[i-],dd=d[i],d1=d[i-];
             if(j<=i-) f[i][j][]=min(f[i-][j][]+dis[c1][cc],(f[i-][j][]+dis[c1][cc])*(1.0-k[i-])+(f[i-][j][]+dis[d1][cc])*k[i-]);
             else if(j<=i-) f[i][j][]=(f[i-][j][]+dis[c1][cc])*(1.0-k[i-])+(f[i-][j][]+dis[d1][cc])*k[i-];
             if(j==i) f[i][j][]=0x7ffffff;
             if((f[i-][j-][]+dis[c1][cc])*(1.0-k[i])+(f[i-][j-][]+dis[c1][dd])*k[i]-0.000000001>((f[i-][j-][]+dis[c1][dd])*(1.0-k[i-])+(f[i-][j-][]+dis[d1][dd])*k[i-])*k[i]+((f[i-][j-][]+dis[c1][cc])*(1.0-k[i-])+(f[i-][j-][]+dis[d1][cc])*k[i-])*(1.0-k[i]))
             {
                 f[i][j][]=(f[i-][j-][]+dis[c1][cc])*(1.0-k[i-])+(f[i-][j-][]+dis[d1][cc])*k[i-];
                 f[i][j][]=(f[i-][j-][]+dis[c1][dd])*(1.0-k[i-])+(f[i-][j-][]+dis[d1][dd])*k[i-];
             }
             else
             {
                 f[i][j][]=f[i-][j-][]+dis[c1][cc];
                 f[i][j][]=f[i-][j-][]+dis[c1][dd];
             }
             if(j==)
             {
                 f[i][j][]=f[i-][j-][]+dis[c1][cc];
                 f[i][j][]=f[i-][j-][]+dis[c1][dd];
                 continue;
             }
         }
     }
     double ans=f[n][][];
     for(int i=;i<=m;i++)
     {
         ans=min(ans,min(f[n][i][],f[n][i][]*(1.0-k[n])+f[n][i][]*k[n]));
     }
     printf("%.2lf\n",ans);
     //while(1);
     return ;
 }