KdTree && Octree 原理学习对比以及可视化分析--"索引树"

1. Kdtree 原理

k-d树（k-dimensional树的简称），是一种分割k维数据空间的数据结构。主要应用于多维空间关键数据的搜索（如：范围搜索和最近邻搜索）；

---

索引结构中相似性查询有两种基本的方式：
(1). "范围查询" ：给定查询点和查询距离的阈值，从数据集中找出所有与查询点距离小于阈值的数据；
(2). "K近邻查询" ：K近邻查询是给定查询点及正整数K，从数据集中找到距离查询点最近的"K"个数据，当K=1，则为[最近邻查询]；

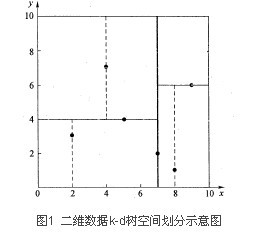
• Kdtree 算法原理（啰嗦，冗长，以下只分析伪码，想看完整的知识扫盲可以看百度百科。。）

  

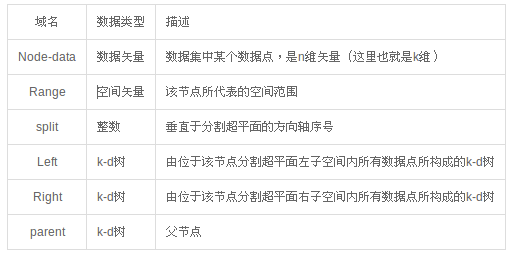
  Q1: 构建k-d树（createKDTree)
      输入：数据点集Data-set和其所在的空间Range
      输出：Kd，类型为k-d tree
  
  "核心算法流程"
      1). 确定split域：对于所有描述子数据（特征矢量），统计它们在每个维上的数据方差。数据方差大表明沿该坐标轴方向上的数据分散得比较开，在这个方向上进行数据分割有较好的分辨率；
      2). 确定Node-data域：数据点集Data-set按其第split域的值排序。位于正中间的那个数据点被选为Node-data,新的点集DataSets去除Node-data点；
      3). 以中间点Node-data为标准，小于Node-data[split]化为左点集，大于Node-data[split]化为右点集；
      4). 左右两边分别建立k-d tree, 即递归调用createKDTree;
  
  Q2: 数据查找，检索在k-d树中与查询点距离最近的数据点
  
      1） 从root节点开始，DFS搜索直到叶子节点，同时在stack中顺序存储已经访问的节点。
      2） 如果搜索到叶子节点，当前的叶子节点被设为最近邻节点。
      3） 然后通过stack回溯:
      4） 如果当前点的距离比最近邻点距离近，更新最近邻节点.
      5） 然后检查以最近距离为半径的圆是否和父节点的超平面相交.
      6） 如果相交，则必须到父节点的另外一侧，用同样的DFS搜索法，开始检查最近邻节点。
      7） 如果不相交，则继续往上回溯，而父节点的另一侧子节点都被淘汰，不再考虑的范围中.
      8） 当搜索回到root节点时，搜索完成，得到最近邻节点。
  

2.Octree原理

Octree即为八叉树，它的特性为树中的任一节点的子节点恰好只会有八个或零个。经常应用于3D场景管理，它可以迅速搜索物体在3D场景中的位置，或侦测到与其他物体是否有碰撞以及判断是否在可视范围内。

"算法原理简介"
    八叉树是一种用于描述三维空间的树状数据结构。八叉树的每个节点表示一个正方体的体积元素，每个节点有八个子节点，将八个子节点所表示的体积元素加在一起就等于父节点的体积。
"算法流程"
    (1). 设定最大递归深度
    (2). 找出场景的最大尺寸，并以此尺寸建立第一个立方体
    (3). 依序将单位元元素丢入能被包含且没有子节点的立方体
    (4). 若没有达到最大递归深度，就进行细分八等份，再将该立方体所装的单位元元素全部分担给八个子立方体
    (5). 若发现子立方体所分配到的单位元元素数量不为零且跟父立方体是一样的，则该子立方体停止细分，因为跟据空间分割理论，细分的空间所得到的分配必定较少，若是一样数目，则再怎么切数目还是一样，会造成无穷切割的情形。
    (6). 重复3，直到达到最大递归深度。

3.PCL中源代码测试

"Kdtree"
/*
* kdtree:
* 是一种分割K维数据空间的数据结构，主要应用于多维空间关键数据的搜索
* （范围搜索 + 最近邻搜索）
*                                           Author: Ian
*/

#include <pcl/point_cloud.h>
#include <pcl/io/pcd_io.h>
#include <pcl/kdtree/kdtree_flann.h>

#include <iostream>
#include <vector>

using namespace std;

int main(int argc, char** argv)
{

    string inputfile = argv[1];

    pcl::PointCloud<pcl::PointXYZ> xyzCloud;
    pcl::PointCloud<pcl::PointXYZRGBA> rgbCloud;

    pcl::io::loadPCDFile<pcl::PointXYZ> (inputfile, xyzCloud);
    cout<<"input cloud's size ="<<xyzCloud.points.size()<<endl;

    pcl::KdTreeFLANN<pcl::PointXYZ> kdtree;
    kdtree.setInputCloud(xyzCloud.makeShared());

    pcl::PointXYZ searchPoint;

//  取点云数据的中间点
    searchPoint = xyzCloud.points[xyzCloud.points.size()/2];

// k nearest neighbor search
    int K=10;
    std::vector<int> pointIdxNKNSearch(K);
    std::vector<float> pointNKNSquaredDistance(K);

    if(kdtree.nearestKSearch (searchPoint, K, pointIdxNKNSearch, pointNKNSquaredDistance) > 0)
    {
        std::cout<<"pointIdxNKNSearch.size ="<<pointIdxNKNSearch.size()<<std::endl;

        for (size_t i = 0; i < pointIdxNKNSearch.size(); ++i)
        std::cout << "    "  <<   xyzCloud.points[ pointIdxNKNSearch[i] ].x
                    << " " << xyzCloud.points[ pointIdxNKNSearch[i] ].y
                    << " " << xyzCloud.points[ pointIdxNKNSearch[i] ].z
                    << " (NKN-squared distance: " << pointNKNSquaredDistance[i] << ")" << std::endl;
    }
//  Neighbors within radius search

  std::vector<int> pointIdxRadiusSearch;
  std::vector<float> pointRadiusSquaredDistance;

  float radius = 0.3f;

    if (kdtree.radiusSearch(searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance) > 0)
    {
        std::cout<<"pointIdxRadiusSearch.size = "<<pointIdxRadiusSearch.size()<<std::endl;
        for (size_t i = 0; i < pointIdxRadiusSearch.size(); ++i)
        std::cout << "   "  <<   xyzCloud.points[ pointIdxRadiusSearch[i] ].x
                    << " " << xyzCloud.points[ pointIdxRadiusSearch[i] ].y
                    << " " << xyzCloud.points[ pointIdxRadiusSearch[i] ].z
                    << " (Radius-squared distance: " << pointRadiusSquaredDistance[i] << ")" << std::endl;
    }

    return 0;
}

"Octree"
    /*
* Octree --八叉树， 用于快速查询物体在3D场景中的位置，或侦测
*       与其他物体是否有碰撞以及是否在可视范围内。
*                                           Author: Ian
*/

#include <pcl/point_cloud.h>
#include <pcl/io/pcd_io.h>
#include <pcl/octree/octree_search.h>

#include <iostream>
#include <vector>

int main(int argc, char**argv)
{
    pcl::PointCloud<pcl::PointXYZ>::Ptr xyzCloud(new pcl::PointCloud<pcl::PointXYZ>);

    std::string inputfile = argv[1];
    pcl::io::loadPCDFile<pcl::PointXYZ> (inputfile, *xyzCloud);
    std::cout<<"inputPCD's size ="<<xyzCloud->points.size()<<std::endl;

    float resolution = 0.01f;
    pcl::octree::OctreePointCloudSearch<pcl::PointXYZ> octree(resolution);

    octree.setInputCloud(xyzCloud);
    octree.addPointsFromInputCloud();

    pcl::PointXYZ searchPoint;
    searchPoint = xyzCloud->points[xyzCloud->points.size()/2];

    std::vector<int> pointIdxVec;

    if(octree.voxelSearch (searchPoint, pointIdxVec))
    {
        std::cout << "Neighbors within voxel search at (" << searchPoint.x
        << " " << searchPoint.y
        << " " << searchPoint.z << ")"
        << std::endl;

        std::cout<<"voxelSearch size = "<<pointIdxVec.size()<<std::endl;

        for (size_t i = 0; i < pointIdxVec.size (); ++i)
            std::cout << "    " << xyzCloud->points[pointIdxVec[i]].x
                << " " << xyzCloud->points[pointIdxVec[i]].y
                << " " << xyzCloud->points[pointIdxVec[i]].z << std::endl;
    }

    // K nearest neighbor search

    int K = 10;

    std::vector<int> pointIdxNKNSearch;
    std::vector<float> pointNKNSquaredDistance;

    if(octree.nearestKSearch (searchPoint, K, pointIdxNKNSearch, pointNKNSquaredDistance) > 0)
    {
        for (size_t i = 0; i < pointIdxNKNSearch.size (); ++i)
        std::cout << "    "  <<   xyzCloud->points[ pointIdxNKNSearch[i] ].x
                    << " " << xyzCloud->points[ pointIdxNKNSearch[i] ].y
                    << " " << xyzCloud->points[ pointIdxNKNSearch[i] ].z
                    << " (NKN-squared distance: " << pointNKNSquaredDistance[i] << ")" << std::endl;
    }

    // Neighbors within radius search

    std::vector<int> pointIdxRadiusSearch;
    std::vector<float> pointRadiusSquaredDistance;

    float radius = 0.3f;

    std::cout << "Neighbors within radius search at (" << searchPoint.x
        << " " << searchPoint.y
        << " " << searchPoint.z
        << ") with radius=" << radius << std::endl;

    if (octree.radiusSearch (searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance) > 0)
    {
        for (size_t i = 0; i < pointIdxRadiusSearch.size (); ++i)
            std::cout << "    "  <<   xyzCloud->points[ pointIdxRadiusSearch[i] ].x
                        << " " << xyzCloud->points[ pointIdxRadiusSearch[i] ].y
                        << " " << xyzCloud->points[ pointIdxRadiusSearch[i] ].z
                        << " (Radius-squared distance: " << pointRadiusSquaredDistance[i] << ")" << std::endl;
    }

    return 0;
}

4.Octree可视化分析

• 因为我想研究三维地图中的柱体图形怎么实时更新，但是我去用pcl_visualization和opengl实现画不同形状的柱体图时，无法满足其实时性能。然后我发现octree的立体分割有点相关的意思，在研究octree可视化案例之后，是否可以将一样大小的立方体改为针对不同障碍物具有不同高度的立方体。这样就能一眼看出障碍物的高度？

• 论文中的图形示例（我没在学校这篇论文下不下来...抱歉）

  

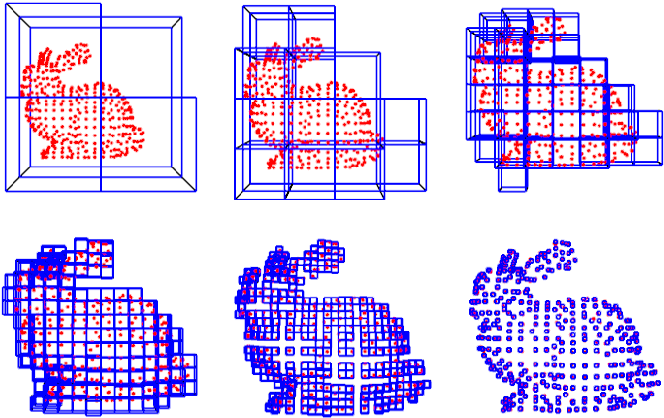
• 参考论文实现的pcl_octree可视化

  

• 以及刚开始靠自己理解用opengl画的柱体地图

  

参考链接

[1]. K-dtree 百度百科

[2]. Octree 百度百科