luogu题解 P3388 【【模板】割点（割顶）】

外加定义：在一个无向图中，如果删掉点 x 后图的连通块数量增加，则称点 x 为图的割点。

外加图示

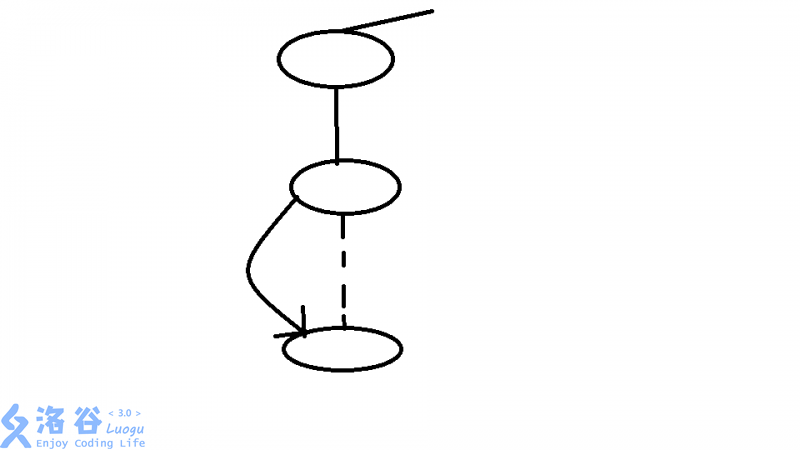
开始思路为割桥上的点为割点，后来证明的确正确。

不过可惜的是他的逆定理错了（gg了），不过数据很弱以至于得了90分。

如图所示

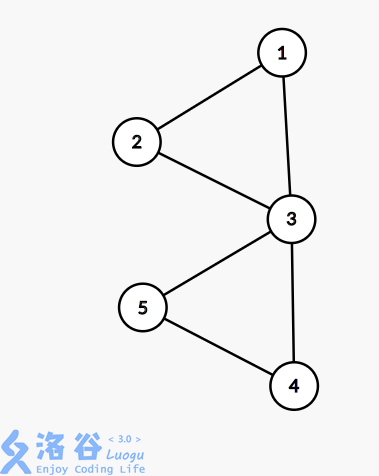
图中无割桥，但点3却是割点，貌似无法解决。

（顺及客串my blog

，以及图论的必要工具

回归正题，另一种思路诞生了：

如果u点的子节点为v，v点他能返回的最老祖先比u点年轻或一样（即dfn[u]值<=low[v]），那么如果删去u点，那么v以下的点就会与v以上的点失去联系，就会产生新的连通块（实质是在我的原来思路上多了一个判断

也就是说如果在我们的搜索树上有一个点只有树边与祖先相连，而没有反向边连回祖先节点的话，那么它就是割点。就是没有这样的边

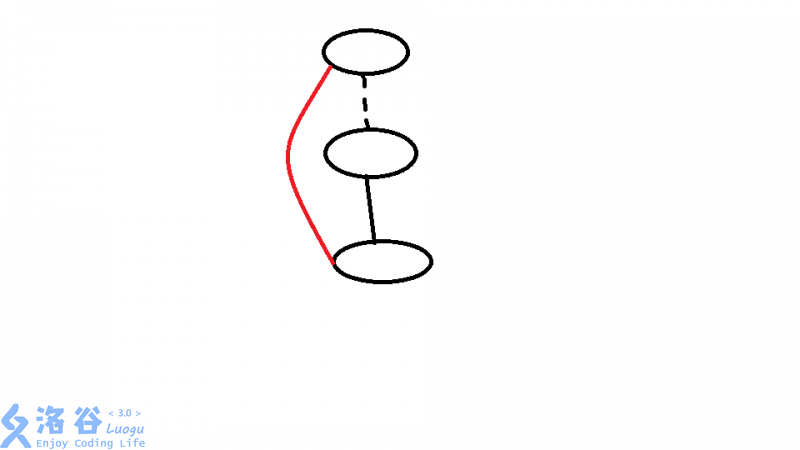
至于实现方法貌似蒟蒻所知只有Tarjan。

这道题是模板题，大家还是不要抄代码为好。（事关今后的Tarjan生涯）

代码

#include<cstdio>
#include<algorithm>
#include<stack>
#include<cstring>
#define Max 1000000+199
using namespace std;
int n,m,dfn[Max]={0},low[Max],cast[Max],ins[Max],inx=0,head[Max],v[Max]={0},cnt=0,gs=0,cd[Max]={0};
stack<int> s;
struct edge
{
	int c,to,next;
}e[Max];
void adde(int a,int b)
{
	cnt++;
	e[cnt].to=b;
	e[cnt].c=a;
	e[cnt].next=head[a];
	head[a]=cnt;
	cd[a]++;
}
int ans=0,gd[Max]={0};
void tarjan(int x,int fa)
{
	int u,sk=0;
	inx++;
	dfn[x]=low[x]=inx;
	s.push(x);
	ins[x]=1;
	for(int i=head[x];~i;i=e[i].next)
	{
		u=e[i].to;
		if(dfn[u]==0)
		{
			tarjan(u,fa);
			if(low[u]>=dfn[x]&&x!=fa)gd[x]=1;
			v[i]=v[i%2==0?i-1:i+1]=1;
			low[x]=min(low[x],low[u]);
			if(x==fa)sk++;
		}
		else if(ins[u]==1&&v[i]==0)v[i]=v[i%2==0?i-1:i+1]=1,low[x]=min(low[x],dfn[u]);
	}
	if(dfn[x]==low[x])
	{
		gs++;
		u=Max;
		while(u!=x)
		{
			u=s.top();
			s.pop();
			ins[u]=0;
			cast[u]=gs;
			//printf("%d %d\n",u,gs);
		}

	}
	if(x==fa&&sk>=2)gd[x]=1;
}
int main()
{
	memset(cd,0,sizeof(cd));
	memset(head,-1,sizeof(head));
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		adde(a,b);
		adde(b,a);
		//printf("%d",v[i]);
	}
	for(int i=1;i<=n;i++)
	if(dfn[i]==0)tarjan(i,i);
	for(int i=1;i<=n;i++)
	{
		if(gd[i]==1)ans++;
	}
	printf("%d\n",ans);
	for(int i=1;i<=n;i++)
	{
		if(gd[i]==1)printf("%d ",i);
	}
	return 0;
}