opencv边缘检测-拉普拉斯算子

sobel算子一文说了,索贝尔算子是模拟一阶求导,导数越大的地方说明变换越剧烈,越有可能是边缘.



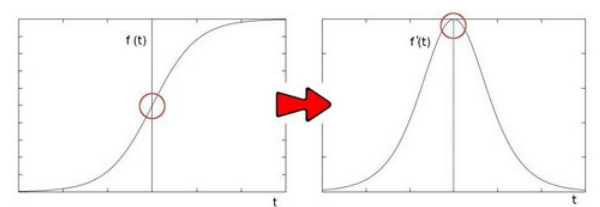
那如果继续对f'(t)求导呢?

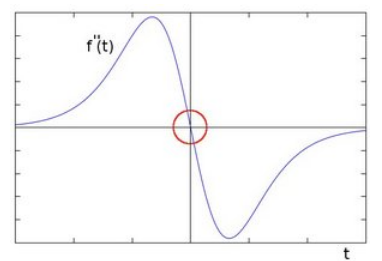
可以发现"边缘处"的二阶导数=0. 我们可以利用这一特性去寻找图像的边缘. 注意有一个问题,二阶求导为0的位置也可能是无意义的位置

拉普拉斯算子推导过程

以x方向求解为例:

一阶差分：f'(x) = f(x) - f(x - 1)

二阶差分：f''(x) = f'(x+1) - f'(x) = (f(x + 1) - f(x)) - (f(x) - f(x - 1))

化简后：f''(x) = f(x - 1) - 2 f(x)) + f(x + 1)

提取前面的系数：[1, -2, 1]

同理得到y方向的系数[1,-2,1]

这样的话,叠加起来就得到了拉普拉斯矩阵

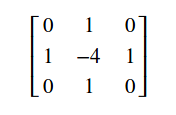
opencv实现

Laplacian api

默认的ksize=1,和ksize=3效果是一样的,都是用的上述拉普拉斯矩阵去卷积原图像

关于filter具体是什么,可以通过函数getDerivKernels得到



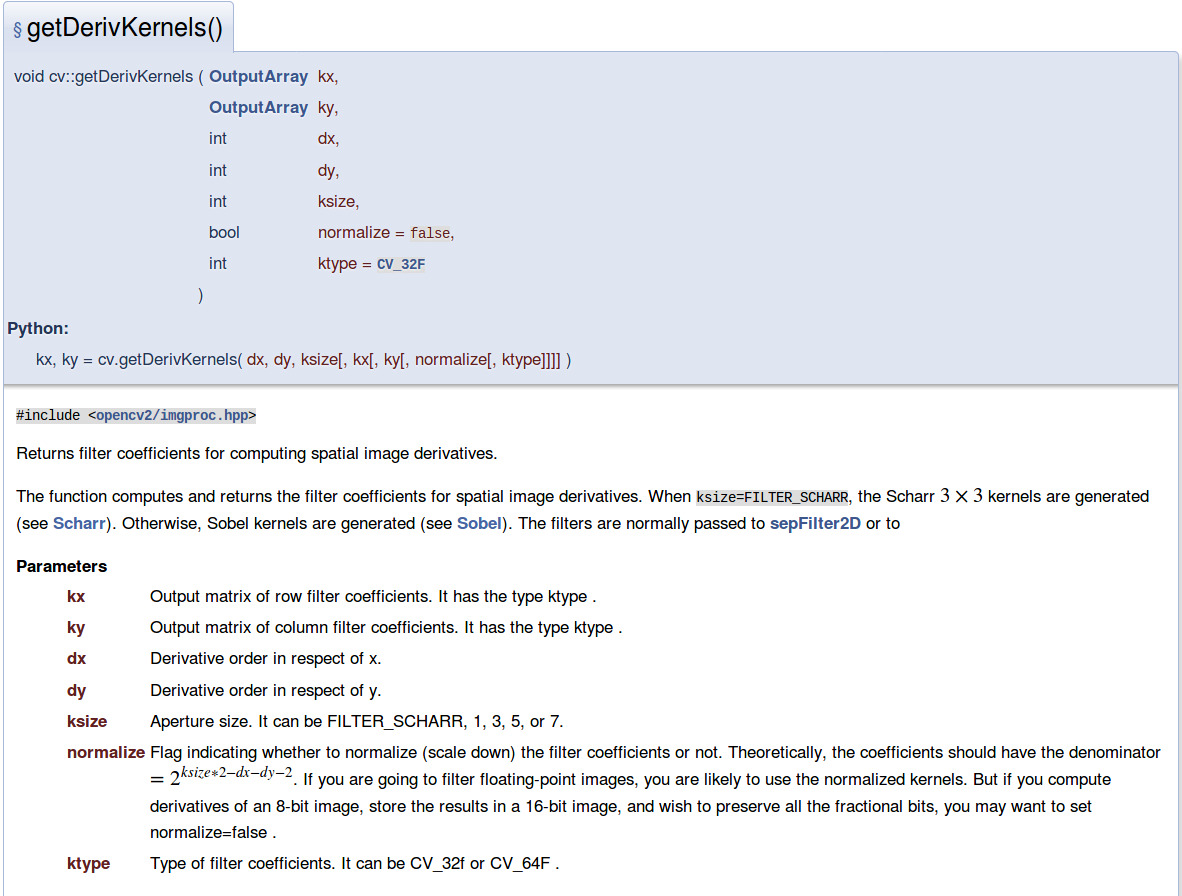
dx,dy代表求导的阶数.

def cal_filter(dx,dy,ksize):
    kx, ky=cv.getDerivKernels(dx, dy, ksize)
    print(kx)
    print(ky)
cal_filter(2,2,1)
cal_filter(2,2,3)
cal_filter(2,2,5)

输出为

可以看到ksize=1和ksize=3其实是一样的.

import cv2 as cv
def test():
    src = cv.imread("/home/sc/disk/keepgoing/opencv_test/sidetest.jpeg")
    src = cv.GaussianBlur(src, (3, 3), 0)
    gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
    dst1 = cv.Laplacian(gray, -1,3)
    dst2 = cv.Laplacian(gray, -1,1)
    cv.imshow("origin",src)
    cv.imshow("dst1",dst1)
    cv.imshow("dst2",dst2)
    if 27 == cv.waitKey():
        cv.destroyAllWindows()
test()

效果如下:

sobel和laplace都是比较简单的边缘检测算法,目前比较常用的是canny,后面的博文会写到.

在搜索各种边缘检测算法的适用场景时,发现大部分文章都只讲了opencv里如何实现,并且都是互相抄来抄去.下面给出个人认为讲的不错的两个link

https://blog.csdn.net/xiaojiegege123456/article/details/7714863

https://dsp.stackexchange.com/questions/74/what-factors-should-i-consider-in-choosing-an-edge-detection-algorithm

二阶导数还可以说明灰度突变的类型。在有些情况下，如灰度变化均匀的图像，只利用一阶导数可能找不到边界，此时二阶导数就能提供很有用的信息。二阶导数对噪声也比较敏感，解决的方法是先对图像进行平滑滤波，消除部分噪声，再进行边缘检测。不过，利用二阶导数信息的算法是基于过零检测的，因此得到的边缘点数比较少，有利于后继的处理和识别工作

总结一下就是:拉普拉斯对噪声更敏感,但是对边缘灰度变化不大的图像,检测效果比索贝尔算子要好一些.比如下图中牛和树的灰度变换并不是特别强.

实际使用中最常用的还是canny算法.后面的博文会再做介绍.