推荐系统(recommender systems):均值归一化(mean normalization)

均值归一化可以让算法运行得更好。

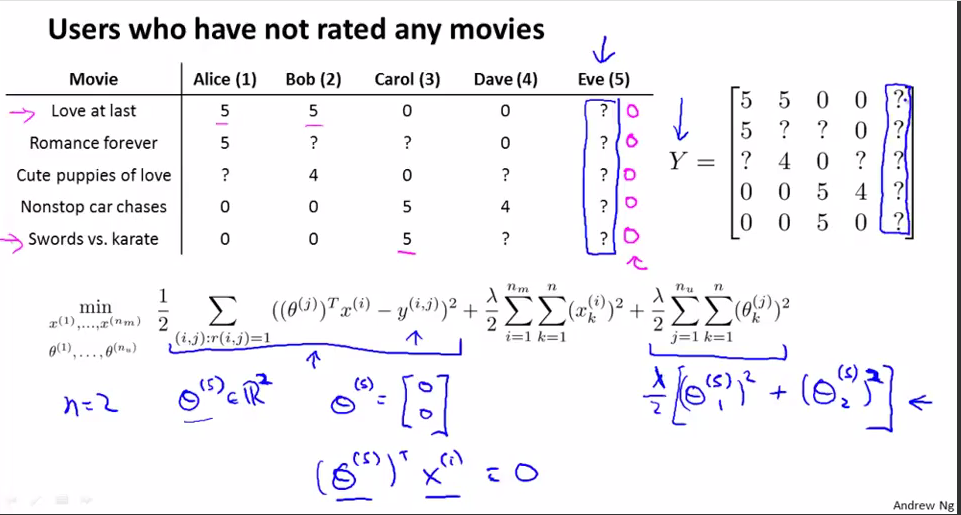
现在考虑这样一个情况：一个用户对所有的电影都没有评分，即上图所示 的Eve用户。现在我们要学习特征向量（假设n=2） 以及用户5的向量θ⁽⁵⁾,因为用户Eve没有对任何电影打分，所以前面的一项为0，只有后面正则化的项，所以影响θ取值的只有后面的θ的正则化的项。所以要使它最小，即θ的取值为0.所以当我们预测用户5对所有电影的评分的时候，这时的评分都为0.所以我们会预测所有的电影的评分都为0.这样是毫无意义的，因为我们还是没有办法知道我们应该向用户5推荐什么电影（没有一部电影评分要高些），所有的电影预测为0也没有意义，因为事实是有的电影评分要高些，有的电影评分要低些。

均值归一化可以让我们解决上面的问题

首先计算每部电影所得评分的均值，将其放在向量u中，将所有的电影评分减去平均评分，即将每部电影的评分归一化，让其平均值变为0.

现在我们将这个评分数据集Y使用协同过滤算法，来学习θ(j)与x(i).

对于用户j对于电影i的评分，我们使用(θ(j))^T(x(i))+u⁽ⁱ⁾

所以对于user5我们学习到的θ为[0,0],这样再加上u值，这样user5对于电影1的预测分为2.5,对于电影2的预测分也为2.5....它的意思其实是在说，如果用户5没有给任何电影评分，我们要做的是预测他对每部电影的评分为这些电影的平均得分

均值归一化Y，使得每行的平均值为0，如果有些电影是没有评分的，这种情况我们可以将Y的列进行均值归一化，但是这种情况可能不好，因为当一部电影没有一个用户对它进行评分时，这种情况我们是不会将这部电影推荐给用户的。所以当用户没有对一部电影进行评分时，我们可以使用行无值归一化来处理，这种情况比列均值归一化要常见些

总结

协同过滤算法的预处理过程--均值归一化，根据数据集的不同，可以让算法运行得更好