常州模拟赛d7t1 亲戚

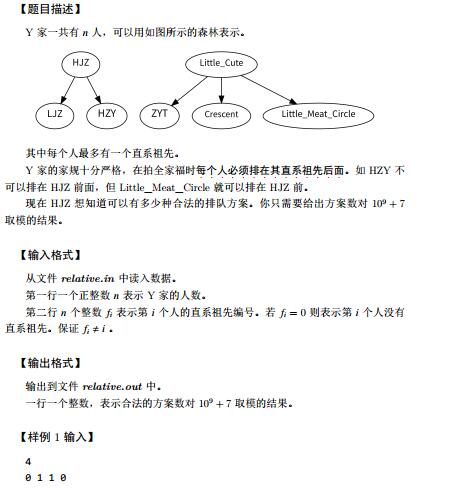
分析：把题目换个方式理解，就是把各个点排成一列，并且指定了若干对的先后次序，问你有多少种序列满足要求.

　　　显然是一道dp题，直接推出方程似乎有点点困难，那么先看看数据特点.

1.有一些点满足fi=0，那么直接输出n!就可以了.

2.保证所有的关系是一条链.我们假设所有链的长度和为sum,链1的长度为l1,链2的长度为l2......

现在有sum个位置，我要把链1上的点按照次序放到sum个位置上，一共有C(sum,l1)种方案，接下来放链2，还有sum - l1个位置，所以有C(sum - l1,l2)种方案，以此类推......

3.保证构成一棵满二叉树.设f[i]表示以i为根的子树的方案数，那么f[i] =C(2s,s)*f[lc]*f[rc],其中s是左右子树的节点数.

下面考虑怎么将这些做法合并为正解的做法.可以先写出一个伪状态转移方程：f[i] = ∏ f[i.son] * i.son的排列方式。这个时候把链换成了子树，其实原理还是一样的.

然后因为要用除法取模，所以需要用到逆元，我们可以在求出阶乘的同时线性求出逆元和逆元的阶乘以便计算组合数.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = ,mod = 1e9+;

int n,fa[maxn],head[maxn],nextt[maxn * ],to[maxn * ],tot = ,sizee[maxn];
long long ans,niyuan[maxn],jiecheng[maxn],nijie[maxn];

void add(int x, int y)
{
    to[tot] = y;
    nextt[tot] = head[x];
    head[x] = tot++;
}

long long C(int x, int y)
{
    return jiecheng[y] * nijie[x] % mod * nijie[y - x] % mod;
}

long long solve(int u)
{
    if (sizee[u] == )
        return ;
    long long res = , sum = sizee[u] - ;
    for (int i = head[u]; i; i = nextt[i])
    {
        int v = to[i];
        res = res * C(sizee[v], sum) % mod;
        res = res * solve(v) % mod;
        sum -= sizee[v];
    }
    return res;
}

void dfs(int u)
{
    sizee[u] = ;
    for (int i = head[u]; i; i = nextt[i])
    {
        int v = to[i];
        dfs(v);
        sizee[u] += sizee[v];
    }
}

int main()
{
    scanf("%d", &n);
    for (int i = ; i <= n; i++)
    {
        scanf("%d", &fa[i]);
        add(fa[i], i);
    }
    jiecheng[] = ;
    niyuan[] = ;
    nijie[] = ;
    nijie[] = ;//一定要赋值！
    for (int i = ; i <= n; i++)
    {
        jiecheng[i] = (long long)jiecheng[i - ] * i % mod;
        niyuan[i] = (long long)(mod - mod / i) * niyuan[mod % i] % mod;
        nijie[i] = (long long)nijie[i - ] * niyuan[i] % mod;
    }
    dfs();
    printf("%lld\n", solve());

    return ;
}