P1979 华容道 spfa题解

题目描述

【问题描述】

小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面，华容道是否根本就无法完成，如果能完成，最少需要多少时间。

小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：

在一个 n*m 棋盘上有 n*m 个格子，其中有且只有一个格子是空白的，其余 n*m-1个格子上每个格子上有一个棋子，每个棋子的大小都是 1*1 的；
有些棋子是固定的，有些棋子则是可以移动的；
任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。

游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。

给定一个棋盘，游戏可以玩 q 次，当然，每次棋盘上固定的格子是不会变的，但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次

玩的时候，空白的格子在第 EXi 行第 EYi 列，指定的可移动棋子的初始位置为第 SXi 行第 SYi列，目标位置为第 TXi 行第 TYi 列。

假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

输入输出格式

输入格式：

输入文件为 puzzle.in。

第一行有 3 个整数，每两个整数之间用一个空格隔开，依次表示 n、m 和 q；

接下来的 n 行描述一个 n*m 的棋盘，每行有 m 个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，0 表示该格子上的棋子是固定的，1 表示该格子上的棋子可以移动或者该格子是空白的。接下来的 q 行，每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。

输出格式：

输出文件名为 puzzle.out。

输出有 q 行，每行包含 1 个整数，表示每次游戏所需要的最少时间，如果某次游戏无法完成目标则输出−1。

输入输出样例

输入样例#1：

3 4 2

0 1 1 1

0 1 1 0

0 1 0 0

3 2 1 2 2 2

1 2 2 2 3 2

输出样例#1：

2

-1

说明

【输入输出样例说明】

棋盘上划叉的格子是固定的，红色格子是目标位置，圆圈表示棋子，其中绿色圆圈表示目标棋子。

第一次游戏，空白格子的初始位置是 (3, 2)（图中空白所示），游戏的目标是将初始位置在(1, 2)上的棋子（图中绿色圆圈所代表的棋子）移动到目标位置(2, 2)（图中红色的格子）上。

移动过程如下：

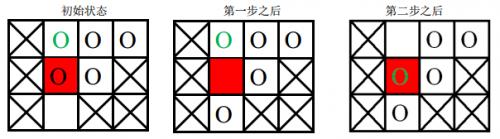
第二次游戏，空白格子的初始位置是（1, 2）（图中空白所示），游戏的目标是将初始位置在（2, 2）上的棋子（图中绿色圆圈所示）移动到目标位置 (3, 2)上。

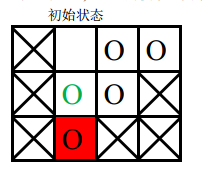
要将指定块移入目标位置，必须先将空白块移入目标位置，空白块要移动到目标位置，必然是从位置（2， 2）上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置，游戏无

法完成。

【数据范围】

对于 30%的数据，1 ≤ n, m ≤ 10，q = 1；

对于 60%的数据，1 ≤ n, m ≤ 30，q ≤ 10；

对于 100%的数据，1 ≤ n, m ≤ 30，q ≤ 500。

我本来是爆搜的但只能有70分，所以要优化一些

先把空白块，到每一个位置的最短路求一下记录方向，再走一遍spfa。

当然，要记得东西很多，很麻烦，比70分的多了好几个数量级

#include<iostream>

#include<algorithm>

#include<cstdio>

#include<cmath>

#include<cstring>

#include<queue>

using namespace std;

const int maxn=,oo=0x3f3f3f3f;

const int dx[]={-,,,},dy[]={,,,-};

int n,m,cas;

int ex,ey,sx,sy,tx,ty;

int a[maxn][maxn],s[maxn][maxn][][],f[maxn][maxn][];

bool visit[maxn][maxn][],map[maxn][maxn];

struct note{

    int x,y,d;

}q[maxn*maxn*];

void bfs(int x,int y)

{

    bool visit[maxn][maxn];

    memset(visit,,sizeof(visit));

    queue<int> p,q;

    p.push(x);

    q.push(y);

    visit[x][y]=;

    while (! q.empty())

    {

        int u=p.front();

        int v=q.front();

        p.pop();q.pop();

        for (int i=;i<=;i++)

        {

            int tx=u+dx[i];

            int ty=v+dy[i];

            if ( map[tx][ty] && a[tx][ty]>a[u][v]+ )

            {

                a[tx][ty]=a[u][v]+;

                if (visit[tx][ty]) continue;

                visit[tx][ty]=;

                p.push(tx);

                q.push(ty);

            }

        }

        visit[u][v]=;

    }

}

void first()

{

    memset(s,0x3f,sizeof(s));

    for (int i=;i<=n;i++)

      for (int j=;j<=m;j++)

        if (map[i][j])

          for (int k=;k<=;k++)

          {

            int x=i+dx[k];

            int y=j+dy[k];

            if (x> && x<=n && y> && y<=m && map[x][y])

            {

                map[x][y]=;

                memset(a,0x3f,sizeof(a));

                a[i][j]=;

                bfs(i,j);

                for (int l=;l<=;l++)

                {

                    int xx=x+dx[l];

                    int yy=y+dy[l];

                    if (xx> && xx<=n && yy> && yy<=m && a[xx][yy]<oo)

                        s[i][j][k][l]=a[xx][yy];

                }

                map[x][y]=;

            }

          }

}

void spfa(int l,int r)

{

    int x,y,xx,yy,d;

    while (l<=r)

    {

        x=q[l].x;

        y=q[l].y;

        d=q[l].d;

        xx=x+dx[d];

        yy=y+dy[d];

        for (int i=;i<=;i++)

        {

            if ((s[x][y][d][i]!=oo)&&(f[xx][yy][i]>f[x][y][d]+s[x][y][d][i]))

            {

                f[xx][yy][i]=f[x][y][d]+s[x][y][d][i];

                if (!visit[xx][yy][i])

                {

                    visit[xx][yy][i]=;

                    q[++r].x=xx;

                    q[r].y=yy;

                    q[r].d=i;

                }

            }

        }

        l++;

        visit[x][y][d]=;

    }

}

int main()

{

    scanf("%d%d%d",&n,&m,&cas);

    for (int i=;i<=n;i++)

    for (int j=;j<=m;j++)

        scanf("%d",&map[i][j]);

    first();

    for(int k=;k<=cas;k++)

    {

        scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty);

        if (sx==tx && sy==ty)

        {

            printf("0\n");

            continue;

        }

        map[sx][sy]=;

        memset(a,0x3f,sizeof(a));

        a[ex][ey]=;

        bfs(ex,ey);

        int l=,r=;

        memset(f,0x3f,sizeof(f));

        memset(visit,,sizeof(visit));

        for (int i=;i<=;i++)

        {

            int x=sx+dx[i];

            int y=sy+dy[i];

            if (map[x][y] && a[x][y]<oo)

            {

                q[++r].x=sx;

                q[r].y=sy;

                q[r].d=i;

                f[sx][sy][i]=a[x][y];

                visit[sx][sy][i]=;

            }

        }

        spfa(l,r);

        int ans=oo;

        for (int i=;i<=;i++)

          ans=min(ans,f[tx][ty][i]);

        if (ans==oo) printf("-1\n");

          else printf("%d\n",ans);

        map[sx][sy]=;

    }

    return ;

}